从零开始的 STL 实现记录:Container-2.3
前言
相较于 vector 的连续线性空间,list 就显得复杂许多、它的好处是每次插人或删除一个元素,就配置或释放一个元素空间。因此,1ist 对于空间的运用有绝对的精准,一点也不浪费。而且,对于任何位置的元素插入或元素移除,list 永远是常数时间。
———— 《STL源码剖析》侯捷
本篇博客将会分析 STL 中 list 的 sort。值得注意的是,在原始的 MyTinySTL 仓库中,作者 list 部分的实现方式是有些怪异的,包括但不限于:使用了本该出现在 SGI-STL 的 slist 中的 base_ptr 与 node_ptr 来代表 list 的指针、没有实现 transfer 函数、sort 的实现也很繁杂;保险起见,下面的解析均以 SGI-STL 中的实现为准。
sort
在分析 list 的 sort 之前,需要弄清楚一件事情:为什么 list 不能使用 STL 算法中的 sort 函数而是需要在内部设计一个自己的 sort 函数?
很多人以及博客会说:因为 list 维护的并不是一个连续的空间,因此不能使用 STL 的 sort。但实际上,deque 内部也不是连续空间,而是分段式的空间,但 deque 依然可以使用 STL 的 sort。根本原因在于:STL 的 sort 算法只接受 RandomAccessIterator,而 list 的 iterator 为 bidirectionalIterator。因此,list 的排序需要类内部单独实现。
为了实现 sort,需要事先介绍几个 list 中的特殊函数。
transfer & splice & reverse & merge
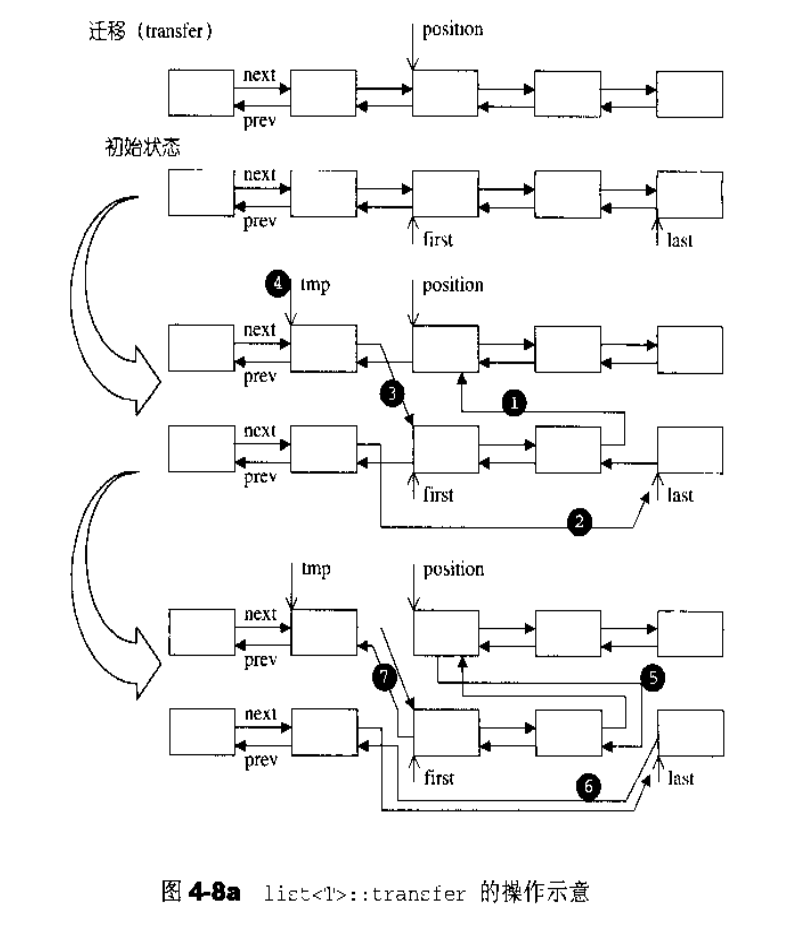
list 内部提供一个所谓的迁移操作 ( transfer ):将某连续范围的元素迁移到某个特定位置之前。技术上很简单,节点间的指针移动而已,这个操作为其它的复杂操作如 splice, sort,merge 等奠定良好的基础。
1 | void transfer(iterator pos, iterator first, iterator last) { |
以上每一步的操作示意如下图所示:
上述的 transfer 并非公开接口,list 公开提供的是所谓的接合操作 ( splice );将某连续范围的元素从一个 list 移动到另一个(或同一个)list 的某个定点。
1 | template <class T, class Alloc = alloc> |
可以看出,splice 提供了多个版本的接口,且内部均调用了 transfer。
merge函数是将传入的list链表x与原链表按从小到大合并到原链表中(前提是两个链表都是已经从小到大排序了)。这里 merge的核心就是 transfer 函数。
1 | template <class T, class Alloc> |
reverse函数是实现将链表翻转的功能. ,将每一个元素一个个插入到begin之前,内部也是利用了 transfer。
1 | template <class T, class Alloc> |
sort 他来了
在实现 list 的过程中原本以为这个 sort 函数就是一个简单的归并排序,就直接复制粘贴了。直到今天写博客才发现,居然看不懂它的实现,一番分析之后顿时惊为天人!不得不感叹 stl 的魅力,仅用十几行的代码就完成了 链表非递归方式的归并排序。趁我还能看懂,赶紧分析一下这个的实现。
在分析之前,需要讲清楚一些函数的作用:
splice:splice函数上面已经分析过,将一个链表中的一部分移动到另一个链表的指定位置之前,这里需要注意的是,被移动的部分确确实实的与原始链表断开了连接,并且插入在了新的链表中。merge: 这个函数上面也进行了分析,将两个有序链表进行合并,由于内部调用的是transfer,与splice相同,如l1.merge(l2),那么合并之后 l2 为空,节点全部被合并至 l1。swap: 这个函数我们没有分析,但不难想象,由于 list 仅有一个成员变量 node(有的版本会有size),因此只需交换两个链表的对应node迭代器就行,l1.swap(l2)相当于将 l1 的全部节点都交给 l2,l2 的全部节点都交给 l1。
下面开始分析这惊为天人的代码。
1 | template <class T> |
首先,如果元素个数小于等于 1,直接返回,这里做特殊处理,没什么好分析的。
1 | if (node_->next == node_ || node_->next->next == node_) return; |
接着定义了一些用于归并排序的变量。
1 | // 一些新的 lists 用于存储分割后的 lists |
其中,carry 负责每次从待排序的 list (以下简称 list)上取下一个节点,并且负责在归并的过程中,在各个 counter 之间搬运节点;counter 为节点的缓存表,用于存放从 list 中取下的节点,缓存表共有 64 层,每一层存放的元素个数符合二进制关系,因此 sort 最多可以处理 2 ^ 64 - 1 个元素;fill 负责维护目前抵达的最深层次,counter[fill] 为空。
下面是一个 while 循环,从条件就可以看出,该算法的做法为每次从 list 上取下一个节点,直到 list 为空即完成了排序。
1 | while (!empty()) |
每次循环都要做三件事公平!公平!还是TMD公平!:
- 开始一次归并的流程,从 list 中取出一个点放进
carry,此时carry必然为空。同时用变量i记录本次归并到达的层数,以用于更新fill与跳出循环。
1 | // 运行到此处 carry 必然为空,因此一定可以处理下一个元素 |
- 从第 0 层(
i维护的层数)开始,逐层进行归并。如果当前遍历到的缓存表中(counter[i])有元素,那么就将counter[i]中的元素与carry合并(由于使用的是merge,保证了有序性),将这一结果交换(swap)给carry,并继续处理下一层。
这里一定要注意:正是
!counter[i].empty()这样的判断条件设计,决定了每一层的counter中元素个数均为2 ^ i,因为如果当前的缓存表counter[i]不为空,那么一定是上一轮的归并将元素移到了当前的缓存表中,这一次直接将其与carry合并,并放入counter[i+1],这不正是二进制的进位操作吗!因此,这样操作下来,counter[i]中的节点个数必然为2 ^ i。
同样道理,如果你想设计一个三进制的counter,只需要将每一层的判断改为 “是否在此之前已经归并了两次” 即可,但是由于二进制的判断最为简单(每个缓存表只有 “空(0)” 与 “满(1)” 两种状态),并且empty很容易判断,因此设计成二进制是最合理的。
1 | // 2. 从小往大不断合并非空层直至遇到空层或者到达当前最大归并层次 |
- 结合上述循环跳出的条件,当前遍历到的缓存表
counter[i]必然是空的,因此需要把carry中携带的所有节点均放进当前的缓存表中(相当于二进制中将这一位置为1)。如果下次依然遍历到了这个表,那么就需要进位了。同时,如果当前已经遍历到了最大层,那么就要更新fill。
1 | // 3. 将合并出的结果放入下一层中 |
跳出了这个外层的循环,就意味着我们已经将链表的节点全部有序地储存在了 counter 中,下面只需要对 counter[0 : fill] 遍历使用 merge 即可完成排序,这里也就不难理解 fill 的设计了,为了方便下面的遍历,并且也满足了 “前闭后开” 的原则。
1 | // 将每一层的 list 依次合并,每一层保证有序 |
最后的 swap(counter[fill - 1]);,是将归并完的结果交换至 list 中,也就完成了排序。
总结
SGI-STL 中的 list 为双向环状链表,只需一个节点便可以遍历整个链表,并且可以轻松维护各种信息(如 begin(), end(), empty() 等)。
相较于 vector,list 的好处是对于任意位置的元素插入与删除,均是常数时间复杂度,且对于空间的使用非常精准,不用像 vector 一样提前分配多余的空间;同时,list 的迭代器也始终有效,不会出现 vector 中的失效情况。但常数时间插入删除元素的代价就是对于任意元素的访问是 O(n) 复杂度。
list 的迭代器为双向迭代器,不支持随机访问,因此也不能使用 STL 中的排序算法对 list 进行排序。为此,list 内部实现了一种十分巧妙的归并排序方法,使用 merge 与 swap 等内部的函数,同时利用了缓存表,实现了时间复杂度 O(nlogn),空间复杂度 O(n) 的归并排序。