前言

红黑树性质：

  1. 节点是红色或黑色。
  2. 根是黑色。
  3. 所有叶子都是黑色（叶子是 NIL 节点）。
  4. 每个红色节点必须有两个黑色的子节点。
  5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

规则类怪谈既视感

从本节开始，将会持续分析 STL 中的红黑树实现，在按照 MyTinySTL 的版本实现了一遍，再看完 STL 源码剖析以及 STL 源码后，感觉这三者的实现都各有不同，而且红黑树太过繁杂，因此这部分的分析有些可能会与 STL 中的实现差别较大。

但博主认为，红黑树这里主要还是理解它的结构与各种操作，简而言之，就是理解 红黑树寄录 这里的内容，虽然是用 python 写的，但也算是完整地实现了红黑树，至于 STL 的话，无非就是在此基础上做了与整个 STL 框架的兼容而已，如 traits、iterator 等，理解思想就好，没必要死磕源码。

本节将会分析红黑树的节点及迭代器的结构设计。

rb-tree 的节点设计

rb-tree 的节点结构分为两层，将节点与数据分开定义，rb_tree_node_base定义指针；rb_tree_node继承前者，增加了数据，就是一个完整的节点。此外，由于红黑树的节点具有颜色的属性，还需定义红黑两种颜色类型。

红黑树的颜色定义

1
2
3
4
5
6
// 红黑树的节点颜色

typedef bool rb_tree_color_type;

static constexpr rb_tree_color_type rb_tree_red = false;   // 红色为 0
static constexpr rb_tree_color_type rb_tree_black = true;  // 黑色为 1

红黑树节点定义，这里与 STL 库中的实现略有不同，没有将 minmum() 与 maxmum() 定义在节点的内部，而是定义为了全局函数，其实这样会有些不妥，这两个函数确实应该定义在节点内部，有空的话再改回 STL 中的逻辑吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
template <class T>
struct rb_tree_node_base {
    typedef rb_tree_color_type                  color_type;
    typedef rb_tree_node_base<T>*               base_ptr;
    typedef rb_tree_node<T>*                    node_ptr;

    base_ptr   parent;      // 父节点
    base_ptr   left;        // 左子节点
    base_ptr   right;       // 右子节点
    color_type color;       // 节点颜色
};

template <class T>
struct rb_tree_node : public rb_tree_node_base<T> {
    typedef rb_tree_node_base<T>*              base_ptr;                
    typedef rb_tree_node<T>*                   node_ptr;

    T value;  // 节点的值
};
1
2
3
4
5
6
7
8
9
10
11
12
13
/// @brief 查找最小节点
template <class NodePtr>
NodePtr rb_tree_min(NodePtr x) noexcept {
    while (x->left != nullptr) x = x->left;
    return x;
}

/// @brief 查找最大节点
template <class NodePtr>
NodePtr rb_tree_max(NodePtr x) noexcept {
    while (x->right != nullptr) x = x->right;
    return x;
}

可以看出，红黑树的节点除了 value 与 color 外是有三个指针的，分别为指向父节点的指针与指向左右孩子节点的指针。与一般的二叉树不同，这里的父节点指针是必要的，因为红黑树在插入与删除节点过程中会经常查询某个节点的父节点及祖父节点。

rb-tree 的 traits

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
template <class T, bool>
struct rb_tree_value_traits_imp {
    typedef T key_type;
    typedef T mapped_type;
    typedef T value_type;

    template <class Ty>
    static const key_type& get_key(const Ty& value) {
        return value;
    }

    template <class Ty>
    static const value_type& get_value(const Ty& value) {
        return value;
    }
};

template <class T>
struct rb_tree_value_traits_imp<T, true> {
    typedef typename std::remove_cv<typename T::first_type>::type  key_type;
    typedef typename T::second_type                                mapped_type;
    typedef T                                                      value_type;

    template <class Ty>
    static const key_type& get_key(const Ty& value) {
        return value.first;
    }

    template <class Ty>
    static const value_type& get_value(const Ty& value) {
        return value;
    }
};

template <class T>
struct rb_tree_value_traits {
    static constexpr bool is_map = tinystl::is_pair<T>::value;

    typedef rb_tree_value_traits_imp<T, is_map>     value_traits_type;
    typedef typename value_traits_type::key_type    key_type;
    typedef typename value_traits_type::mapped_type mapped_type;
    typedef typename value_traits_type::value_type  value_type;

    template <class Ty>
    static const key_type& get_key(const Ty& value) {
        return value_traits_type::get_key(value);
    }

    template <class Ty>
    static const value_type& get_value(const Ty& value) {
        return value_traits_type::get_value(value);
    }
};

template <class T>
struct rb_tree_traits {
    typedef rb_tree_value_traits<T>            value_traits;

    typedef typename value_traits::key_type    key_type;
    typedef typename value_traits::mapped_type mapped_type;
    typedef typename value_traits::value_type  value_type;

    typedef value_type*                        pointer;
    typedef const value_type*                  const_pointer;
    typedef value_type&                        reference;
    typedef const value_type&                  const_reference;

    typedef rb_tree_node_base<T>               base_type;
    typedef rb_tree_node<T>                    node_type;

    typedef base_type*                         base_ptr;
    typedef node_type*                         node_ptr;
};

由于需要支持 set 与 map 结构，因此 value_traits 方面必须要能够萃取出 pair 类型中的 first_type 与 second_type，同时也必须支持非 pair 类型元素的萃取。

因此，这里根据 is_map = tinystl::is_pair<T>::value; 来使用不同的 rb_tree_value_traits_imp，也是一种偏特化的技术。关于偏特化详见 Iterator-1，不仅在迭代器的设计中会使用到偏特化，之后还会更加频繁地使用这一思想。

最后，rb_tree 的萃取器由 rb_tree_traits 实现，就是内置了一个 rb_tree_value_traits 并且再定义了一遍相应型别。

rb-tree 的迭代器设计

与节点的设计理念相同，迭代器也分为 rb_tree_iterator_base 与 rb_tree_iterator 两层。其中 rb_tree_iterator_base 实现了迭代器的移动逻辑，而取值等逻辑则在 rb_tree_iterator 中实现。

此外，rb-tree 的迭代器支持前进与后退，支持 ++ 与 -- 运算符，但不支持 +n 与 -n 运算，因此是 bidirectional_iterator 类型。

rb_tree_iterator_base

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
template <class T>
struct rb_tree_iterator_base : public tinystl::iterator<tinystl::bidirectional_iterator_tag, T> {
    typedef typename rb_tree_traits<T>::base_ptr base_ptr;

    base_ptr node;  // 指向 rb-tree 的节点

    rb_tree_iterator_base() : node(nullptr) {}  // 默认构造函数

    // 使迭代器前进
    void inc() {
        if (node->right != nullptr) {
            node = rb_tree_min(node->right);
        }
        // 如果没有右子节点
        else {
            auto p = node->parent;
            while (node == p->right) {
                node = p;
                p = p->parent;
            }
            // // 应对“寻找根节点的下一节点，而根节点没有右子节点”的特殊情况
            if (node->right != p) {
                node = p;
            }
        }
    }

    // 使迭代器后退
    void dec() {
        // 如果 node 为 header，则指向整棵树的 max 节点
        if (node->parent->parent == node && rb_tree_is_red(node)) {
            node = node->right;  // 指向整棵树的 max 节点
        }
        else if (node->left != nullptr) {
            node = rb_tree_max(node->left);
        }
        // 非 header 节点，也无左子节点
        else {
            auto p = node->parent;
            while (node == p->left) {
                node = p;
                p = p->parent;
            }
            node = p;
        }
    }

    bool operator==(const rb_tree_iterator_base& rhs) { return node == rhs.node; }
    bool operator!=(const rb_tree_iterator_base& rhs) { return node != rhs.node; }
};

这里比较令人费解的是 inc() 与 dec() 两个函数的设计，除了正常地找节点的后继节点与前继节点外，还多考虑了其他的情况，这种情况的出现与 STL 中红黑树的设计有关，打开 stl_tree.h，可以看到对于红黑树如下的注释：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// Red-black tree class, designed for use in implementing STL
// associative containers (set, multiset, map, and multimap). The
// insertion and deletion algorithms are based on those in Cormen,
// Leiserson, and Rivest, Introduction to Algorithms (MIT Press,
// 1990), except that
//
// (1) the header cell is maintained with links not only to the root
// but also to the leftmost node of the tree, to enable constant
// time begin(), and to the rightmost node of the tree, to enable
// linear time performance when used with the generic set algorithms
// (set_union, etc.)
//
// (2) when a node being deleted has two children its successor node
// is relinked into its place, rather than copied, so that the only
// iterators invalidated are those referring to the deleted node.

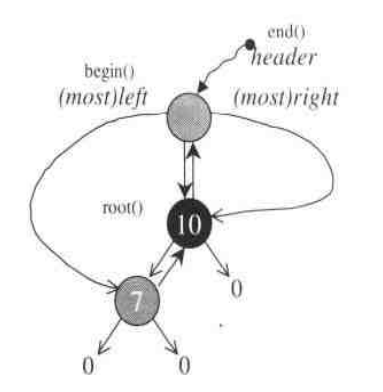
STL 的红黑树在 root 节点之外还有一个 header 节点，该节点与 root 互为父亲节点，header 起到 end 的作用，即标志着已经查找到了最后一个节点，并且在插入与删除节点的过程中维护 header.left 指向红黑树的最小节点，header.right 指向最大节点，当树中仅有 root 时，header.parent = header.left = header.right = root; root.parent = header;。

维护 leftmost 与 rightmost 主要是为了实现常数时间的 begin() 操作以及在使用集合算法时实现线性的复杂度。

了解了这些再来看 inc() 的逻辑：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 使迭代器前进
void inc() {
    if (node->right != nullptr) {
        node = rb_tree_min(node->right);
    }
    // 如果没有右子节点
    else {
        auto p = node->parent;
        while (node == p->right) {
            node = p;
            p = p->parent;
        }
        // // 应对“寻找根节点的下一节点，而根节点没有右子节点”的特殊情况
        if (node->right != p) {
            node = p;
        }
    }
}

特殊情况如下图所示，当寻找根节点的下一节点，而根节点没有右子节点时，会进入 else 分支，并且此时一定满足 node == p->right，因为 header 会维护最大节点，此时一定指向 root；进入 while 循环后王车易位，p 与 node 所指的节点交换，node 指向 header，即代表树的末尾，如果不加下面的特殊判断就会变成迭代器前进后依然等于自身，不符合逻辑。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 使迭代器后退
void dec() {
    // 如果 node 为 header，则指向整棵树的 max 节点
    if (node->parent->parent == node && rb_tree_is_red(node)) {
        node = node->right;  // 指向整棵树的 max 节点
    }
    else if (node->left != nullptr) {
        node = rb_tree_max(node->left);
    }
    // 非 header 节点，也无左子节点
    else {
        auto p = node->parent;
        while (node == p->left) {
            node = p;
            p = p->parent;
        }
        node = p;
    }
}

dec() 的逻辑同理，需要针对 header 特殊处理，当 node 为 header(end) 时，迭代器后退的话就是指向树的最大节点，也就是 header->right 维护的节点。

rb_tree_iterator

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
template <class T>
struct rb_tree_iterator : public rb_tree_iterator_base<T> {
    typedef rb_tree_traits<T>                tree_traits;

    typedef typename tree_traits::value_type value_type;
    typedef typename tree_traits::pointer    pointer;
    typedef typename tree_traits::reference  reference;
    typedef typename tree_traits::base_ptr   base_ptr;
    typedef typename tree_traits::node_ptr   node_ptr;  // link_type

    typedef rb_tree_iterator<T>              iterator;
    typedef rb_tree_const_iterator<T>        const_iterator;
    typedef iterator                         self;

    using rb_tree_iterator_base<T>::node;

    // 构造函数
    rb_tree_iterator() {}
    rb_tree_iterator(base_ptr x) { node = x; }
    rb_tree_iterator(node_ptr x) { node = x; }
    rb_tree_iterator(const iterator& rhs) { node = rhs.node; }
    rb_tree_iterator(const const_iterator& rhs) { node = rhs.node; }

    // 重载操作符
    // reference operator*() const { return node->get_node_ptr()->value; }  // 获得节点的值
    reference operator*()  const { return static_cast<node_ptr>(node)->value; }  // 获得节点的值
    pointer   operator->() const { return &(operator*()); }                       // 获得节点的值的指针

    self& operator++() {
        this->inc();
        return *this;
    }

    self operator++(int) {
        self tmp(*this);
        this->inc();
        return tmp;
    }

    self& operator--() {
        this->dec();
        return *this;
    }

    self operator--(int) {
        self tmp(*this);
        this->dec();
        return tmp;
    }
};

iterator 就是在 iterator_base 的基础上增加了 * 与 -> 的重载，使得迭代器能够取出节点中的数据，并且将 iterator_base 的 inc() 以及 dec() 操作封装成对于 ++ 与 -- 的重载。

rb-tree 的数据结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
/// @brief 模板类 rb_tree
/// @tparam T  节点的值类型
/// @tparam Compare  节点键值比较准则
template <class T, class Compare>
class rb_tree {

public:  // rb_tree 的嵌套型别定义
    typedef rb_tree_traits<T>                               tree_traits;
    typedef rb_tree_value_traits<T>                         value_traits;

    typedef typename tree_traits::base_type                 base_type;
    typedef typename tree_traits::base_ptr                  base_ptr;
    typedef typename tree_traits::node_type                 node_type;
    typedef typename tree_traits::node_ptr                  node_ptr;  // link_type
    typedef typename tree_traits::key_type                  key_type;
    typedef typename tree_traits::mapped_type               mapped_type;
    typedef typename tree_traits::value_type                value_type;
    typedef Compare                                         key_compare;

    typedef tinystl::allocator<T>                           allocator_type;
    typedef tinystl::allocator<T>                           data_allocator;
    typedef tinystl::allocator<base_type>                   base_allocator;
    typedef tinystl::allocator<node_type>                   node_allocator;

    typedef typename allocator_type::pointer                pointer;
    typedef typename allocator_type::const_pointer          const_pointer;
    typedef typename allocator_type::reference              reference;
    typedef typename allocator_type::const_reference        const_reference;
    typedef typename allocator_type::size_type              size_type;
    typedef typename allocator_type::difference_type        difference_type;

    typedef rb_tree_iterator<T>                             iterator;
    typedef rb_tree_const_iterator<T>                       const_iterator;
    typedef tinystl::reverse_iterator<iterator>             reverse_iterator;
    typedef tinystl::reverse_iterator<const_iterator>       const_reverse_iterator;

    allocator_type get_allocator() const { return node_allocator(); }
    key_compare    key_comp()      const { return key_comp_; }

private:  // rb_tree 的数据成员
    base_ptr    header_;      // 特殊节点，与根节点互为父节点
    size_type   node_count_;  // 节点数量
    key_compare key_comp_;    // 节点键值比较准则

private:
    /// @brief 获取根节点
    base_ptr& root()      const { return header_->parent; }
    /// @brief 获取最小节点
    base_ptr& leftmost()  const { return header_->left; }
    /// @brief 获取最大节点
    base_ptr& rightmost() const { return header_->right; }

public:  // 构造、复制、析构函数
    rb_tree() { rb_tree_init(); }

    rb_tree(const rb_tree& rhs);
    rb_tree(rb_tree&& rhs) noexcept;

    rb_tree& operator=(const rb_tree& rhs);
    rb_tree& operator=(rb_tree&& rhs) noexcept;

    ~rb_tree() { clear(); }

public:  // 迭代器相关操作
    iterator                begin()     noexcept        { return leftmost(); }
    const_iterator          begin()     const noexcept  { return leftmost(); }

    iterator                end()       noexcept        { return header_; }
    const_iterator          end()       const noexcept  { return header_; }

    reverse_iterator        rbegin()    noexcept        { return reverse_iterator(end()); }
    const_reverse_iterator  rbegin()    const noexcept  { return const_reverse_iterator(end()); }

    reverse_iterator        rend()      noexcept        { return reverse_iterator(begin()); }
    const_reverse_iterator  rend()      const noexcept  { return const_reverse_iterator(begin()); }

public:  // 容量相关操作
    bool        empty()     const noexcept  { return node_count_ == 0; }
    size_type   size()      const noexcept  { return node_count_; }
    size_type   max_size()  const noexcept  { return static_cast<size_type>(-1); }

public:  // 元素相关操作

public:  // 查找相关操作

private:  // 辅助函数
};

rb-tree 仅由以下三个数据表现。

1
2
3
4
private:  // rb_tree 的数据成员
    base_ptr    header_;      // 特殊节点，与根节点互为父节点
    size_type   node_count_;  // 节点数量
    key_compare key_comp_;    // 节点键值比较准则

使用 header 与特殊的连接设计（见上文），可以很方便地访问到红黑树的头尾节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
private:
    /// @brief 获取根节点
    base_ptr& root()      const { return header_->parent; }
    /// @brief 获取最小节点
    base_ptr& leftmost()  const { return header_->left; }
    /// @brief 获取最大节点
    base_ptr& rightmost() const { return header_->right; }

public:  // 迭代器相关操作
    iterator                begin()     noexcept        { return leftmost(); }
    const_iterator          begin()     const noexcept  { return leftmost(); }

    iterator                end()       noexcept        { return header_; }
    const_iterator          end()       const noexcept  { return header_; }

    reverse_iterator        rbegin()    noexcept        { return reverse_iterator(end()); }
    const_reverse_iterator  rbegin()    const noexcept  { return const_reverse_iterator(end()); }

    reverse_iterator        rend()      noexcept        { return reverse_iterator(begin()); }
    const_reverse_iterator  rend()      const noexcept  { return const_reverse_iterator(begin()); }