图形学补完计划（四）：光照模型-2

参考

0. https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
1. https://zhuanlan.zhihu.com/p/370903314

全局光照模型

上一节主要分析了以 Phong 模型为主的局部光照模型，这些光照模型都是经验性的，不真实的；本节要介绍的全局光照模型就恰好相反。

全局光照模型是基于光学物理原理的，光照强度的计算依赖于光能在现实世界中的传播情况，考虑光线与整个场景中各物体表面及物体表面间的相互影响，是绘制真实感图形的理论依据；具体而言，包括 路径跟踪（path tracing）、双向路径跟踪（bidirectional path tracing）、辐射度方法（radiosity method）等。

与局部光照模型相比，全局光照模型需要相当大的计算量 ，但同时也能取得非常逼真的真实效果。由于计算机硬件的限制，全局光照模型一般在离线渲染领域如电影中应用，随着GPU硬件的发展和算法的改进 ，采用全局照模型的实时渲染逐渐成为研究的热点。

Ray Tracing (Whitted-Style)

光线跟踪算法通过模拟光的传播方式，即光从光源出发经过若干次反射或折射到达摄像机的过程来实现全局光照效果。其思想起源于光线投射算法。由于只有最终到达摄像机的光线才会对生成的图像有贡献，因此光线跟踪的实现通常是从摄像机逆向发出光线，以寻找达到光源的路径。尽管对光线的跟踪方向不同，两者所遵循的计算方式是一致的。其核心操作是寻找光线与场景中物体的交点。

光追的基本假设

基本假设：光线一定沿直线传播；光线之间无法碰撞；光线路径可逆。

实现过程

1. Ray Casting

从人眼或摄像机向近投影平面上的每一个像素点发射一条光线，判断与场景物体的交点。

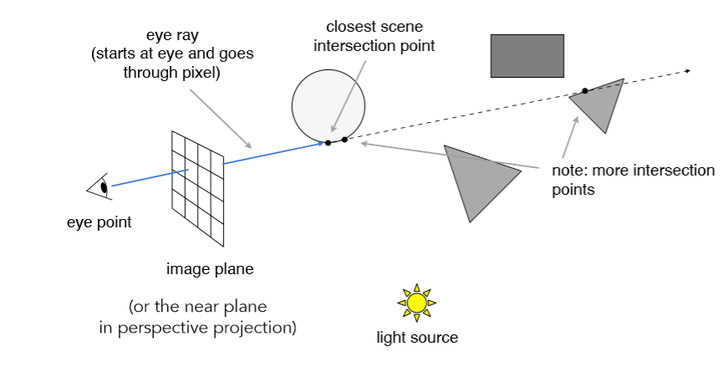
当然一条光线自然可能会与不止一个物体相交，但是考虑遮挡关系，只去找最近的交点。接着连接该交点和光源，只要判断这条连线之间是否有物体存在就可以知道该交点是否在阴影之中。

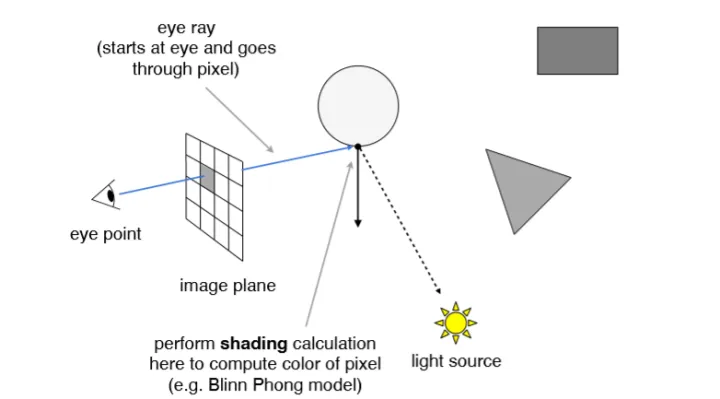
紧接着，自然可以利用着色模型（如Blinn-Phong模型）对这个点进行局部光照模型计算，得到该像素的颜色，那么遍历所有近投影平面上的像素就能得到一张完整的图像。但如果光线追踪仅仅是在第一步Ray Casting就停止的话，那么它的效果与局部光照模型是一样的，因此我们需要第二步，真正的考虑全局效果。

2. Recursive (Whitted-Style) Ray Tracing

除直接接受光源照射的点对该像素点产生的影响外，额外考虑反射、折射等情况；折射与反射之后再与物体相交的点也可以贡献光（光路可逆原理）。简而言之，除了直接从光源照射到物体交点再沿着 primary ray (从眼睛发射的第一条光线) 到眼睛中，也可能存在这样一种情形：有光照射到其他物体，沿着 secondary rays 经过了反射或折射回到 primary ray，再传回人眼。

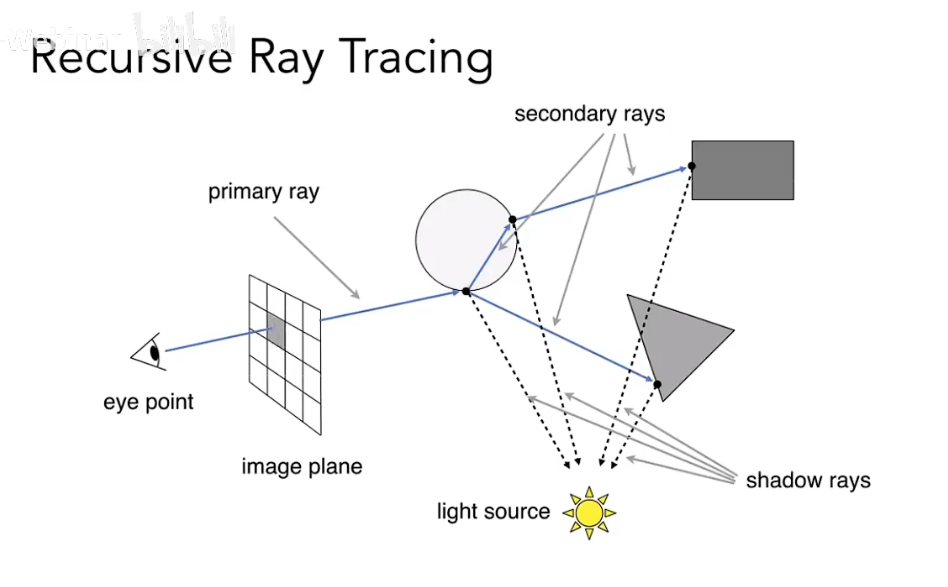
下一步将这些所有交点与光源连接，称这些光线为 shadow rays（因为可以用来检测阴影），计算这些所有点的局部光照模型的结果，将其按照光线能量权重累加，最终得到该像素点的颜色。而这就是一个考虑全局效果的光照模型了，因为不仅仅考虑了直接光源的贡献，还考虑各种折射与反射光线的贡献。

以上就是光线追踪的整个过程了，还有额外几点要注意的 tips：

• 整体过程是一个递归的过程，因此需要一定的递归终止条件，比如说允许的最大反射或折射次数为10。
• 光线在每次反射和折射之后都有能量损耗的，由系数决定，因此越往后的折射和反射光贡献的能量越小，这也是为什么在上文中提到根据光线能量权重求和。 e.g. 反射系数为0.7，那么第一次反射折损 30%，第二次反射折损1-（70%x70%），依次类推。
• 如果反射或折射光线没有碰撞到物体，一般直接返回一个背景色。

一些计算

本文并不打算详细分析光线的具体表达式以及和各种几何形状交点的求解，这部分可以参考 Whitted-Style光线追踪原理详解及实现细节，这里简单列出一些关于光线以及三角形的计算。

1. 如何判断一个点是否在三角形内

   1. 面积法，点划分的三个小三角形面积是否等于大三角形；
   2. 叉乘法，沿逆时针方向，三角形两两顶点构成三个向量，比如AB,BC,CA，分别用这三个向量与起点和P的交点构成的向量求叉乘，如ABxAP, BCxBP, CAxCP，由右手定则，如果三个结果都是正的，说明这个点都在向量的左边；可以推导得出这个点在三角形内，否则只要有一个是负数，就说明在右手边，在三角形外了。

2. 如何判断一条光线是否与一个三角形相交

   1. 先判断光线是否和三角形所在的面相交，再判断这个交点是否在三角形内，判断点是否在三角形内；

   

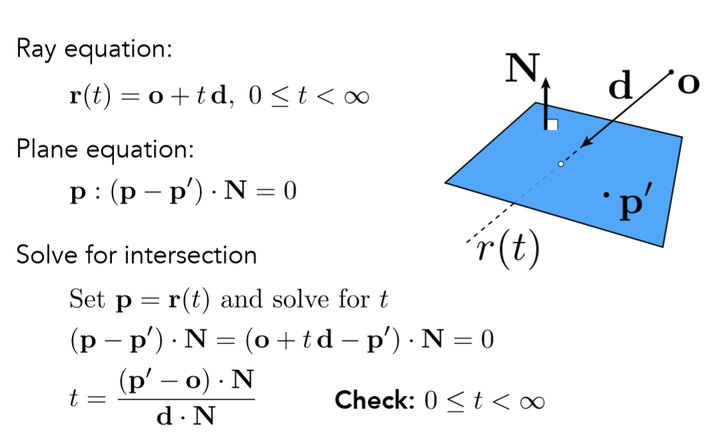
   2. 用Moller Trumbore算法，简称MT算法。(光线的方程是：ray = origin + direction * t) 原理是如果一个点在三角形内，就能用重心坐标系去表示这个点；重心坐标公式，α = 1 – β - λ；带入方程，有3个未知数（β，λ，t），由因为都是三维变量，可以得到三个等式；利用克拉默法则，线性代数的知识，就可以求解出这三个未知数；解出来，判定t是否合理，t > 0，然后α、β和 λ 三个系数都是非负的，就是有解，在三角形内。

   

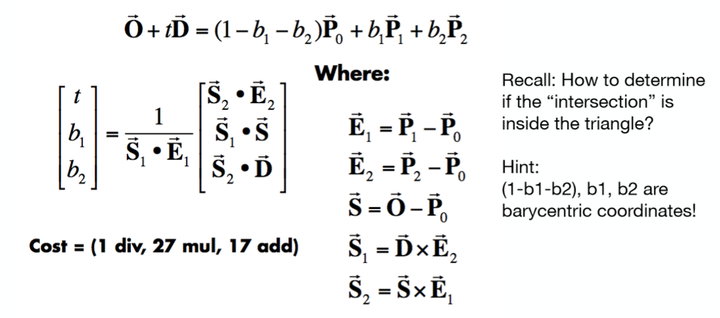
加速计算方法

AABB (Axis-Aligned Bounding Boxes)

使用包围盒可以减少一次光追的计算次数，如果光线与物体的包围盒没有交点，那么和物体上的三角形肯定没有交点，就可以省去这部分的计算。

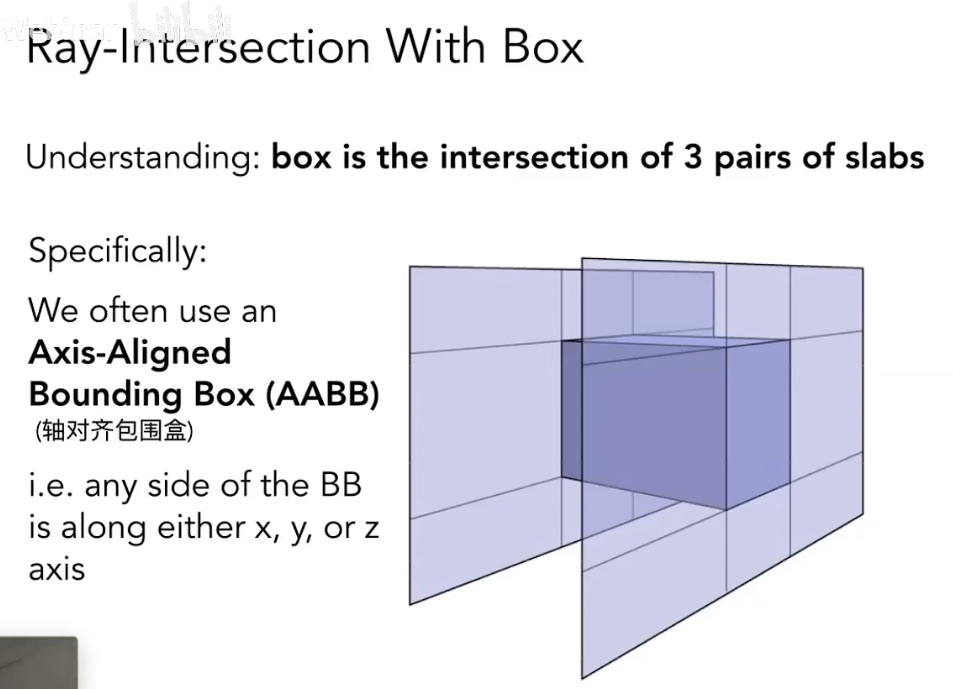
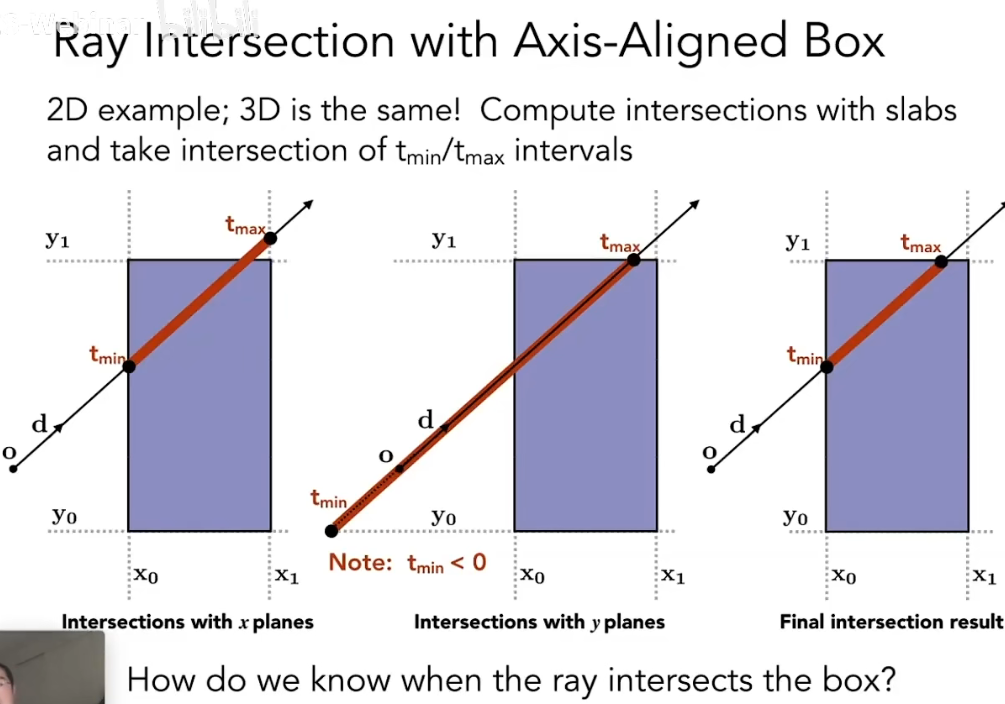
对于一个包围盒为 AABB 的物体而言，当且仅当一条光线的 t_{enter} < t_{exit} && t_{exit} >= 0 时，光线才和该 AABB 有交点，因此才有可能和物体有交点，才需要计算这部分的光照对像素的影响。

空间划分 ( Spatial Partitions )

空间划分也是加速光线与物体求交运算的一种方式，通常与 AABB 一同使用；空间划分可以将空间分割成不同的区域，对于没有物体的区域就不再计算光线与这部分包围盒的交点，从而达到加速计算的效果。

空间划分有多种方式，这里只介绍 KD-Tree。

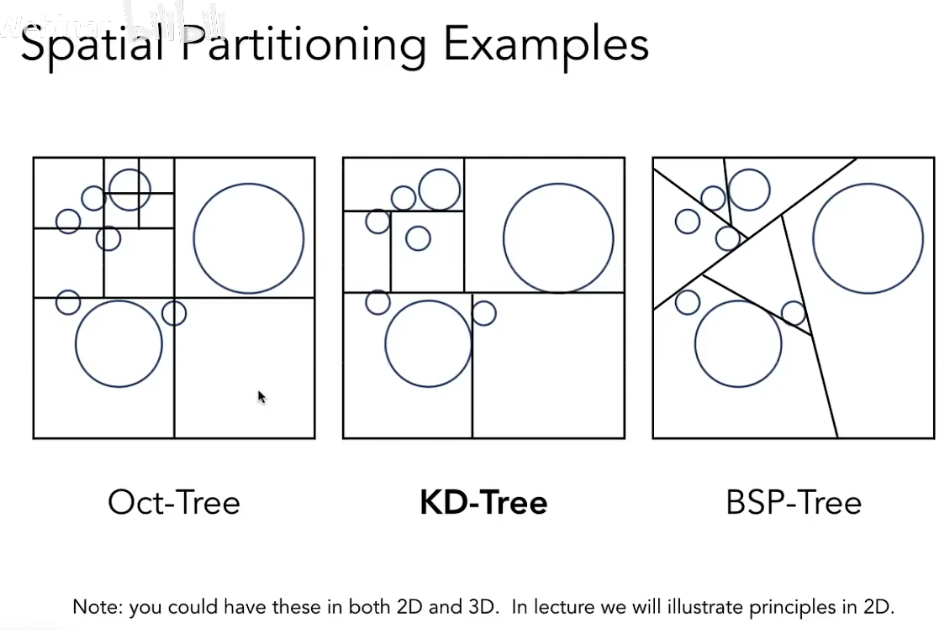
KD-Tree 简称 k维树，是一种空间划分的数据结构。常被用于高维空间中的搜索，比如范围搜索和最近邻搜索。kd-tree是二进制空间划分树的一种特殊情况

KD-Tree 是一个二叉树，只有叶子节点中存放物体的信息，非叶子节点只记录划分信息。

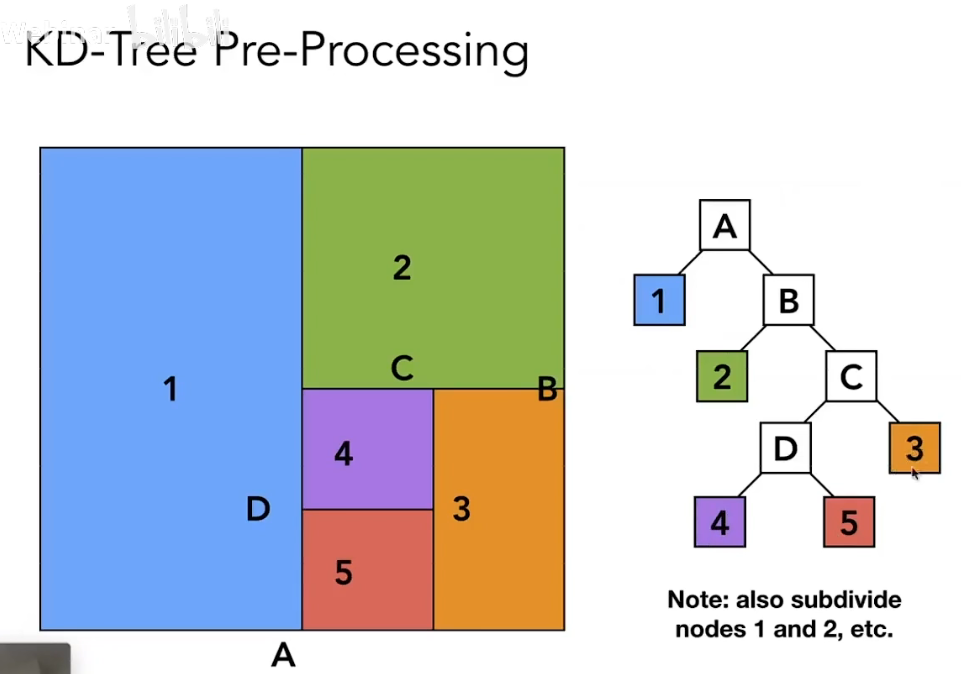
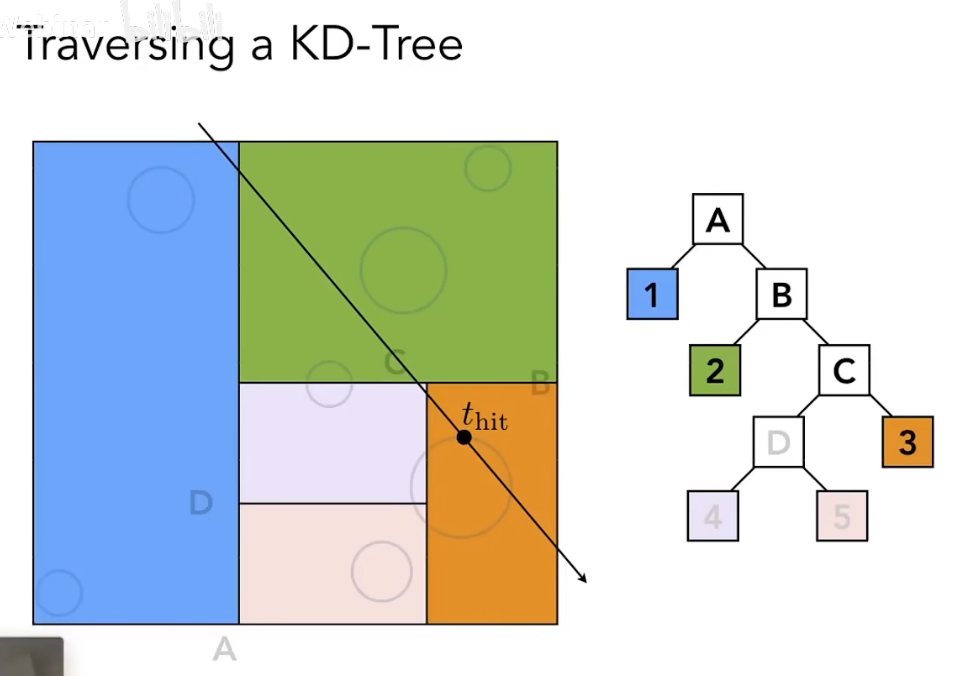
如上图对空间的划分，在光线求交时就省去了区域 5（粉色部分）的计算，达到了加速的效果。

• 存在的问题：空间划分虽然能达到加速的效果，但依然存在一些问题，如：KD-Tee 的建立较为麻烦，三角形是否在一个包围盒内难以判断；一个物体可能同时被划分进了多个包围盒等；

物体划分（Object Partition）

相较于空间划分，物体划分是一种对物体进行分割的方法，会将物体划分为不同的子集，得到的结果被称为 Bounding Volume Hierarchies ( BVH ) 层次包围盒。

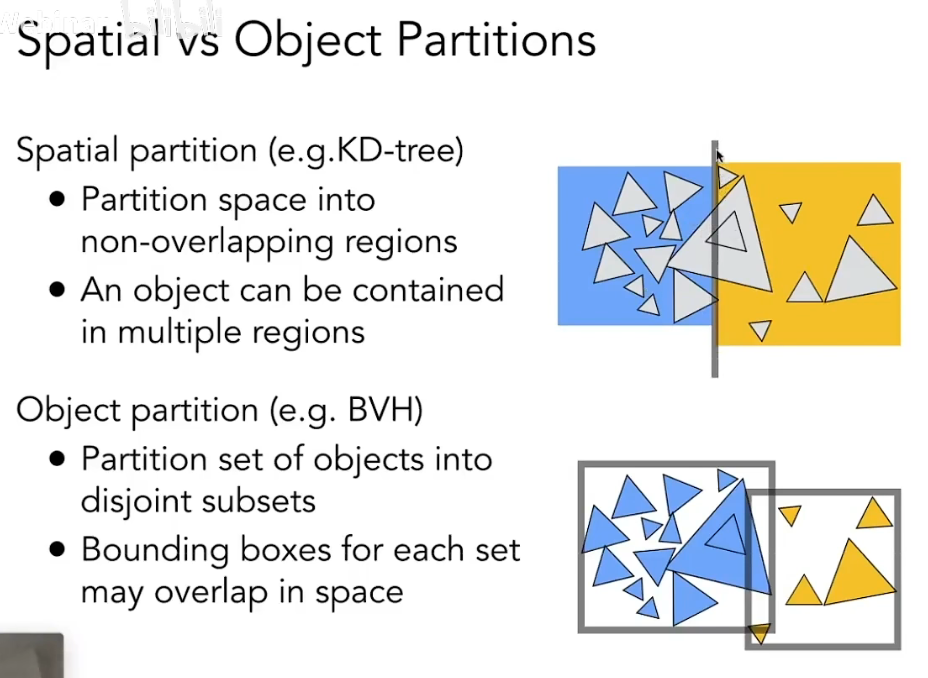
物体划分确保了物体不会同时存在于多个包围盒中，且包围盒比较容易得出（计算三角形的最大最小边坐标），解决了 KD-Tree 存在的一些问题，但同时可以看到，BVH 在空间上的划分是可能会有重叠的

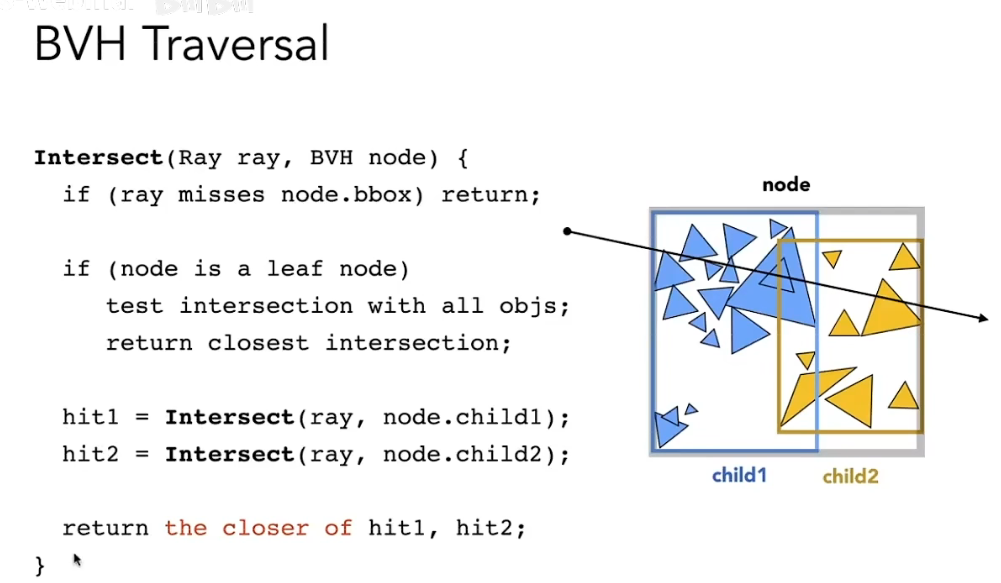
KD-Tree 与 BVH 的优劣

TODO

辐射度量学（Radiometry）

相关概念

1. 辐射能（Radiant Energy）：符号 $Q$，单位 $J$（焦耳）。

2. 辐射通量（Radiant Flux）：符号 $\Phi$，单位 $W$（瓦特）或 $lm$（流明）；表示单位时间内的辐射能。

   

3. 辐射强度(Radiant Intensity)：符号 $I$，单位 $cd$（坎德拉）；表示单位立体角上的辐射通量。

   

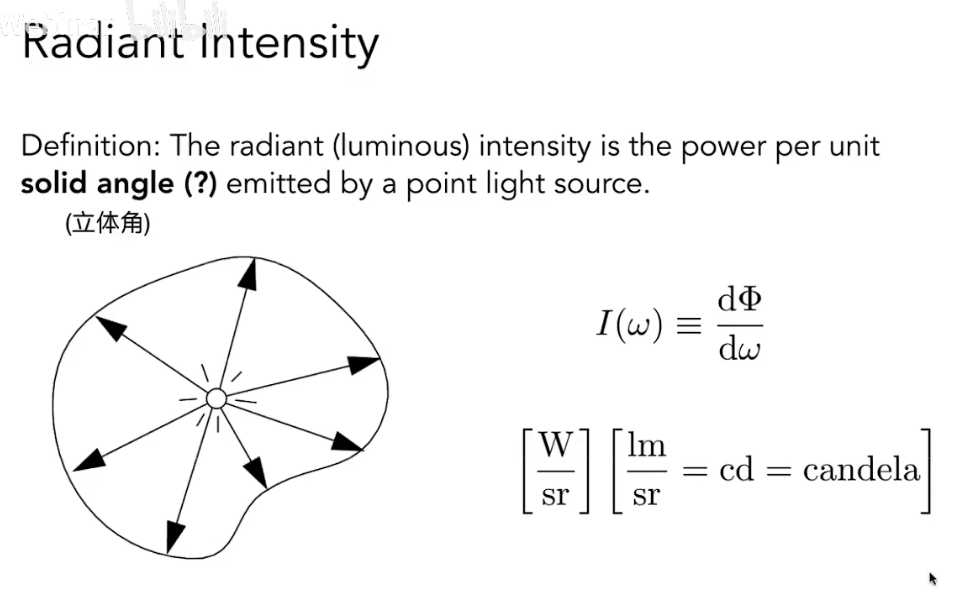
   与辐射强度相关的是立体角的定义：

   

   微分立体角：

   

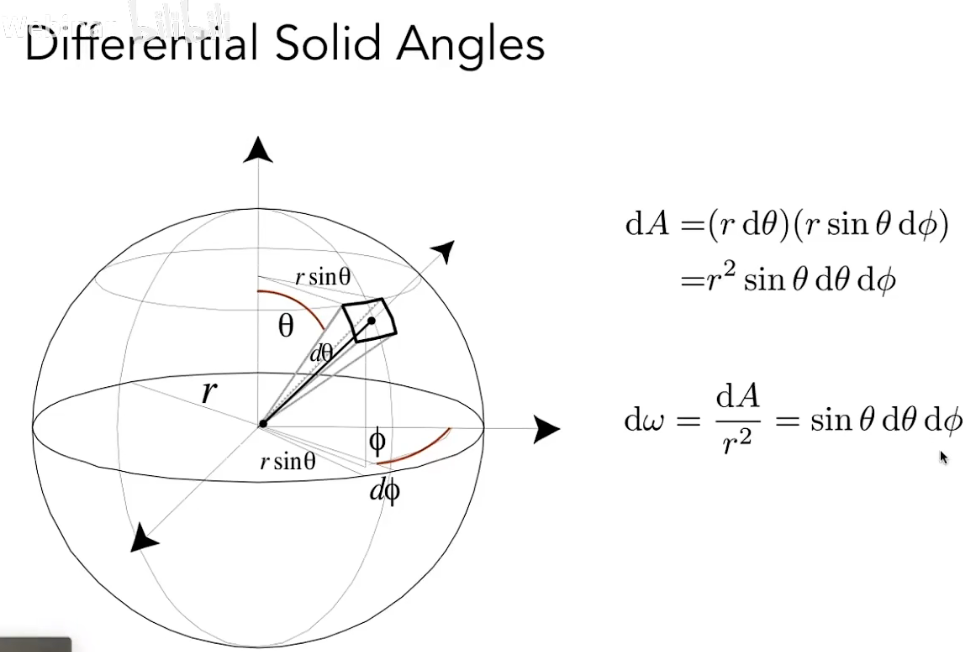
   对于一个球面而言，积分后得到的立体角大小为 $4\pi$。

4. 辐照度(Irradiance)，符号 $E$ ，单位 $lux$（拉克丝），表示单位面积上的辐射通量。

   

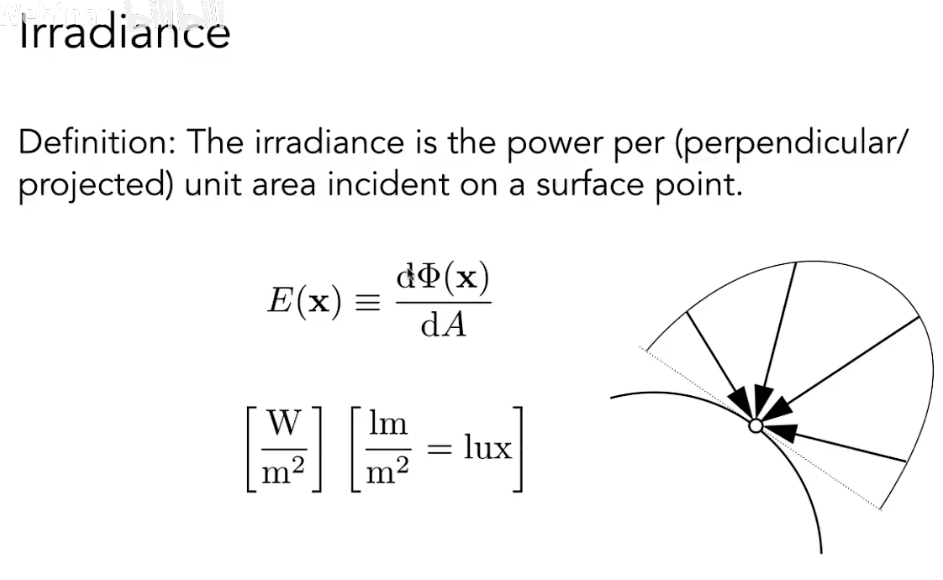
   注意，这里计算面积一定要是投影到光线垂直方向上的面积，与 Lambert 光照模型中相同。

   

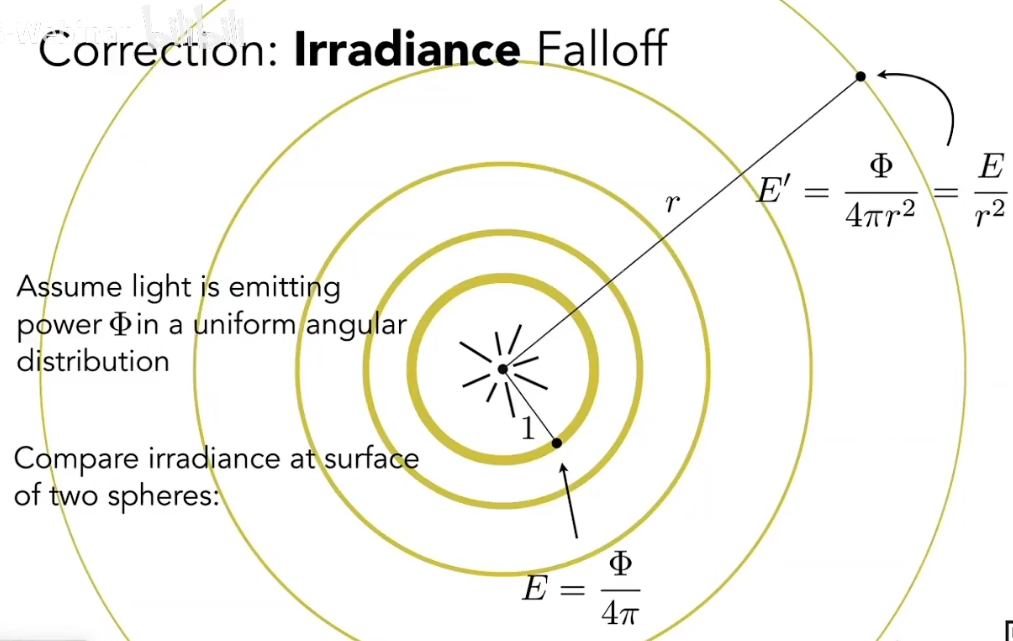
   此外，关于光的能量在传播过程中的衰减，在 Lambert 光照模型中只是定性地进行分析，而这里我们可以分析得出定量的结论：对于一个固定的光源，传播过程中会衰减的是光线的 Irradiance，而 intensity 在此过程中保持不变。

5. 辐射率(Radiance)，符号 $L$，单位 $nit$（尼特），表示单位立体角、单位投影面积上的辐射通量。

   

   

   Radiance 由于是 Flux 分别对于 Solid Angle 与 Area 做了一次微分，而单独对 Solid Angle 微分得到的结果为 Radiant Intensity，单独对 Unit Area 做微分得到的结果为 Irradiance；因此可以分开理解。

   

   以 Irradiance 再对 Solid Angle 微分的思路可以理解为：单位面积往某个特定方向辐射的能量或某个特定方向的入射光线对 dA 贡献的能量。

   

   以 Intensity 再对 Unit Area 微分的思路可以理解为：一束特定光线对于某个特定方向辐射的能量分量。

Irradiance vs. Radiance

式中的 cos 是计算投影面积得到的

辐射度量学中经常涉及的是 Irradiance 和 Radiance 之间的关系。由定义可知，Irradiance 代表的是单位面积上的辐射通量，因此可以理解为单位面积上接收到的能量总量（单位时间），而 Radiance 表示的是单位投影面积、单位角度上的辐射通量，因此可以理解为 “Irradiance 的一部分”，将 Radiance 在能够接收到能量的所有角度范围内进行积分，即可得到 Irradiance。

BRDF

BRDF (Bidirectional Reflectance Distribution Function)，译作双向反射分布函数，是一个用来描述物体表面如何反射光线的方程，表示了当给定一条入射光的时候，某一条特定的出射光线的性质是怎么样的。它的精确定义是出射光辐射率(Radiance)的微分和入射光辐照度(Irradiance)的微分之比。

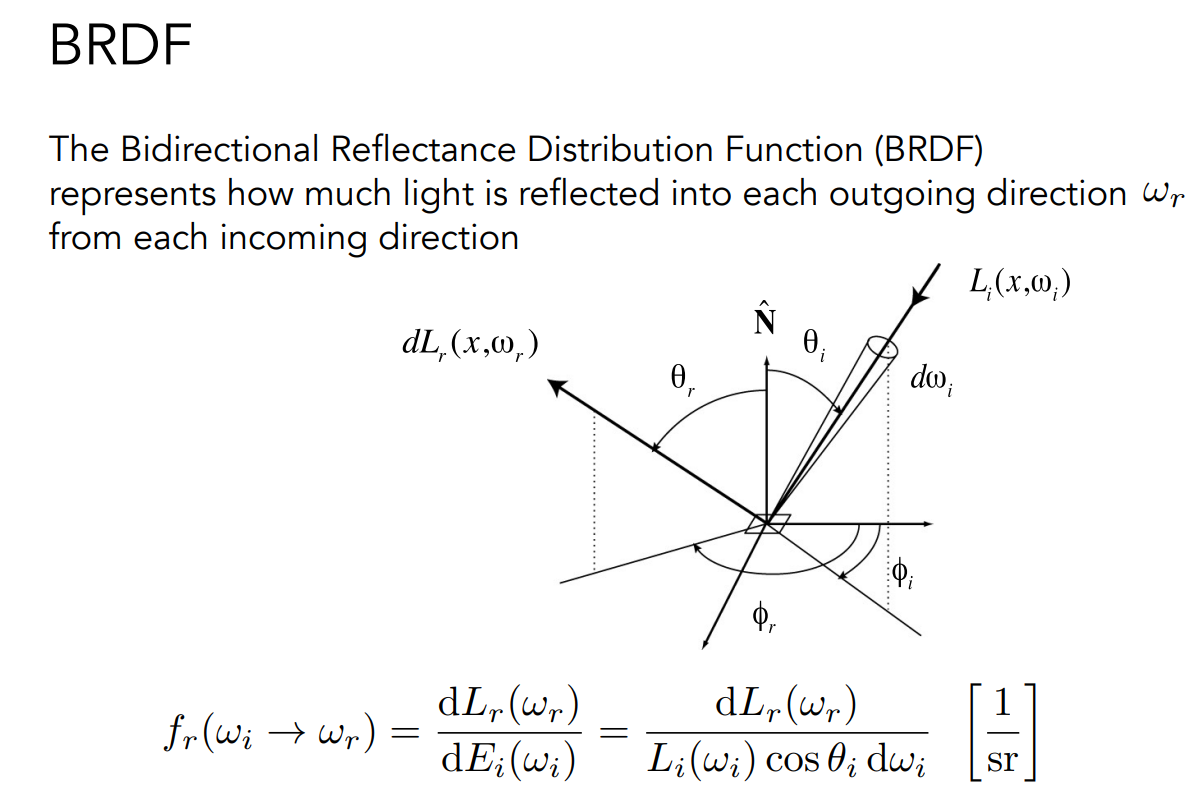
这里一定要注意，BRDF 是出射光的 Radiance 的微分与入射光的 Irradiance 的微分之比，也就是说入射光是对单位投影面积积分了的，因此多了一个微元 $\cos{\theta_i}\mathrm{d} \omega_{i}$。

关于这一点，有很多解释都十分复杂，可以参考 brdf为什么要定义为一个单位是sr-1的量？，我的理解是入射光一定是一个有实际物理 “大小” 的光线，不能简单地将其简化为完全的一维的射线，需要考虑一个微小范围内的光线对单位面积的影响；又因为上面提到的 radiance 与 irradiance 之间的积分关系，计算某一个特定方向的入射光线对该单位面积的贡献，也就相当于一个积分的微元，即 $L_{i}(\omega_{i}) \cos{\theta_i}\mathrm{d} \omega_{i}$。

而出射光线由于这里只是进行数值分析，因此还是将其考虑为完全不存在物理实体的 Irradiance，但如果接着计算该出射光线照射到其他表面，就又要考虑到物理实体，即变成微元，合理。

Reflection Equation

由 BRDF，我们就可以得到反射方程，即：点 p 在 $\omega_{r}$ 方向上的反射光的 Radiance，就等于各个方向入射光的 Radiance 乘以该方向朝 $\omega_{r}$ 的 BRDF 的积分。

一个显然的问题是，由于求一个点反射的 Radiance 需要考虑到所有方向的入射光，而入射光除了光源外还有可能是其他点的反射光，因此这就变成了一个递归的问题。

Rendering Equation

考虑物体的自发光项，将 Reflection Equation 加上 $L_{e}(p, \omega_{o})$ 就得到了渲染方程。

然后经过一系列复杂的推导。。。（这部分还是看 Games 101 Lecture-15 吧）

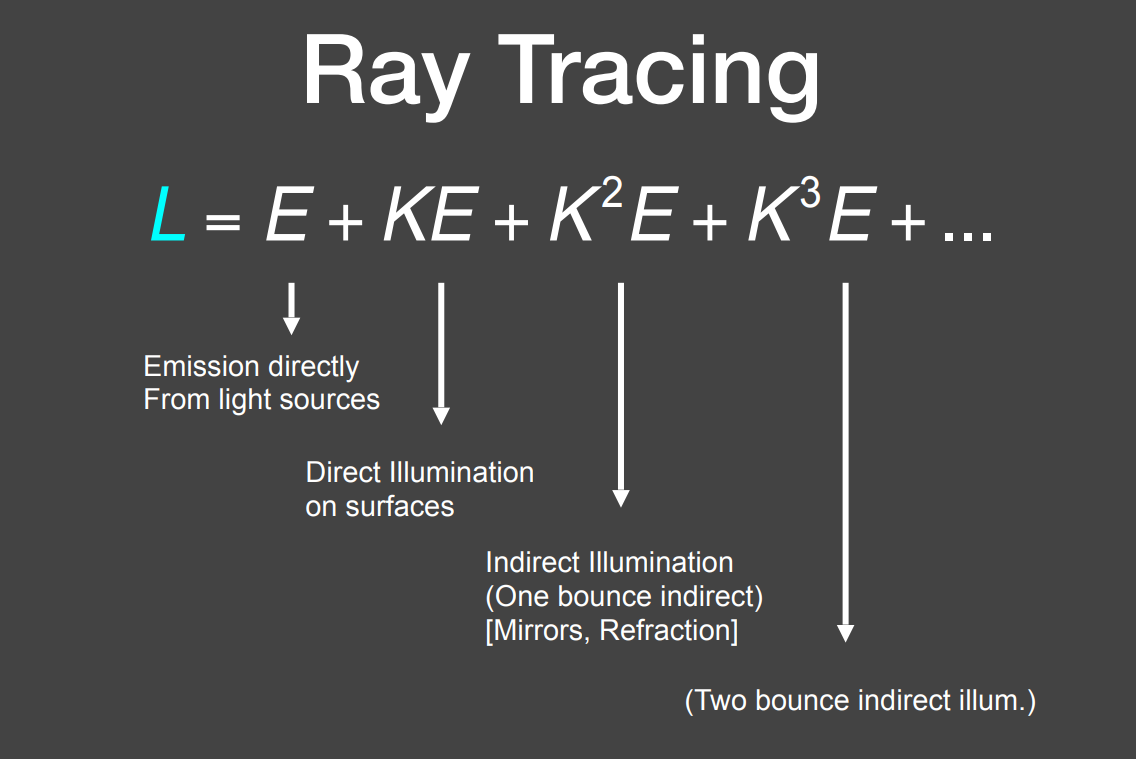
就可以得到这样的形式，即一个点的光照情况等于自发光 + 光源照射光 + 反射光 + 二次反射光 … 无穷项相加的形式。

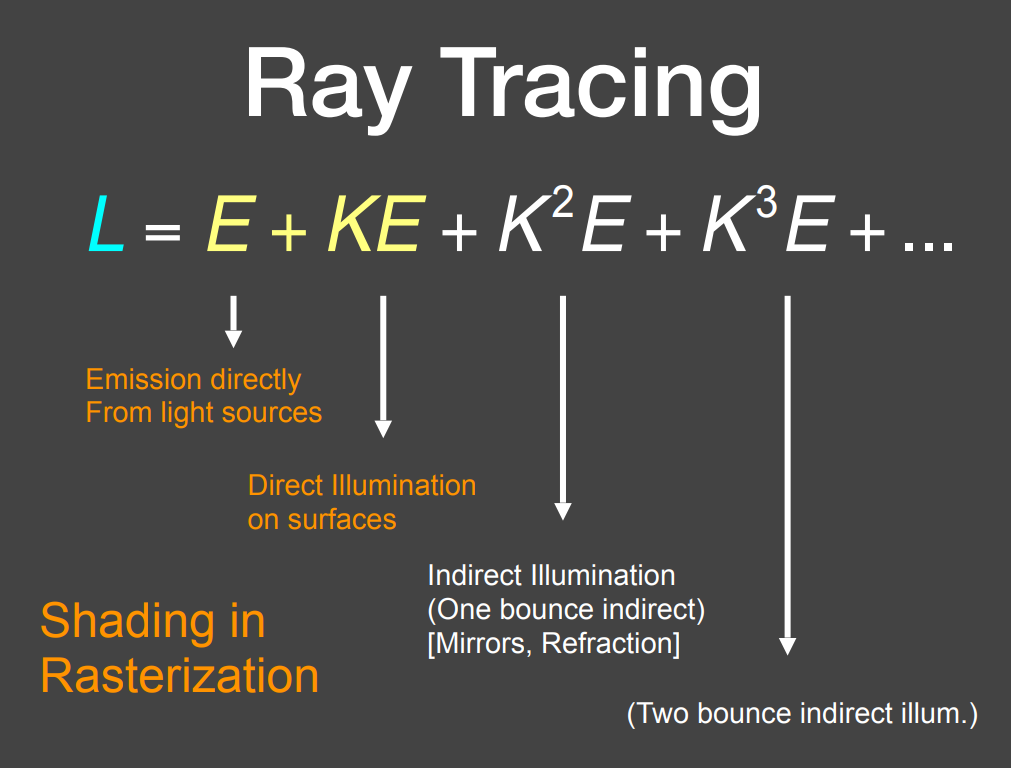
从这个角度考虑，光栅化只计算了渲染方程中的前两项，真实的光照情况需要考虑所有项。

Monte Carlo Path Tracing

Whitted-style ray tracing 存在的问题：任何产生反射的平面都表现出像镜子一样的完全反射效果，对于磨砂材质的物体无法处理；且遇到漫反射表面就直接停止光线的追踪；这肯定是不符合物理规律的。

因此提出了 Path Tracing。

Monte Carlo Integration

蒙特卡洛积分的原理是基于概率统计的思想，通过随机抽样来近似计算数学积分。它的基本思路是，我们可以将要计算的积分问题转化为求解某个概率密度函数下的期望值。具体来说，我们可以将积分问题转化为求解随机变量的期望值，然后通过大量的随机样本来近似计算这个期望值。

需要注意的是：

1. 采样点数越多，计算得到的方差越小
2. 必须要在积分域上采样

Path Tracing

考虑对以上渲染方程进行求解（忽略自发光项）

使用蒙特卡洛积分法对点 p 所能接收到光（radiance）的半球范围内进行积分

可以得到上述的结果与伪代码；当然，上式仅考虑了光源的直接光照，如何求解间接光照呢？

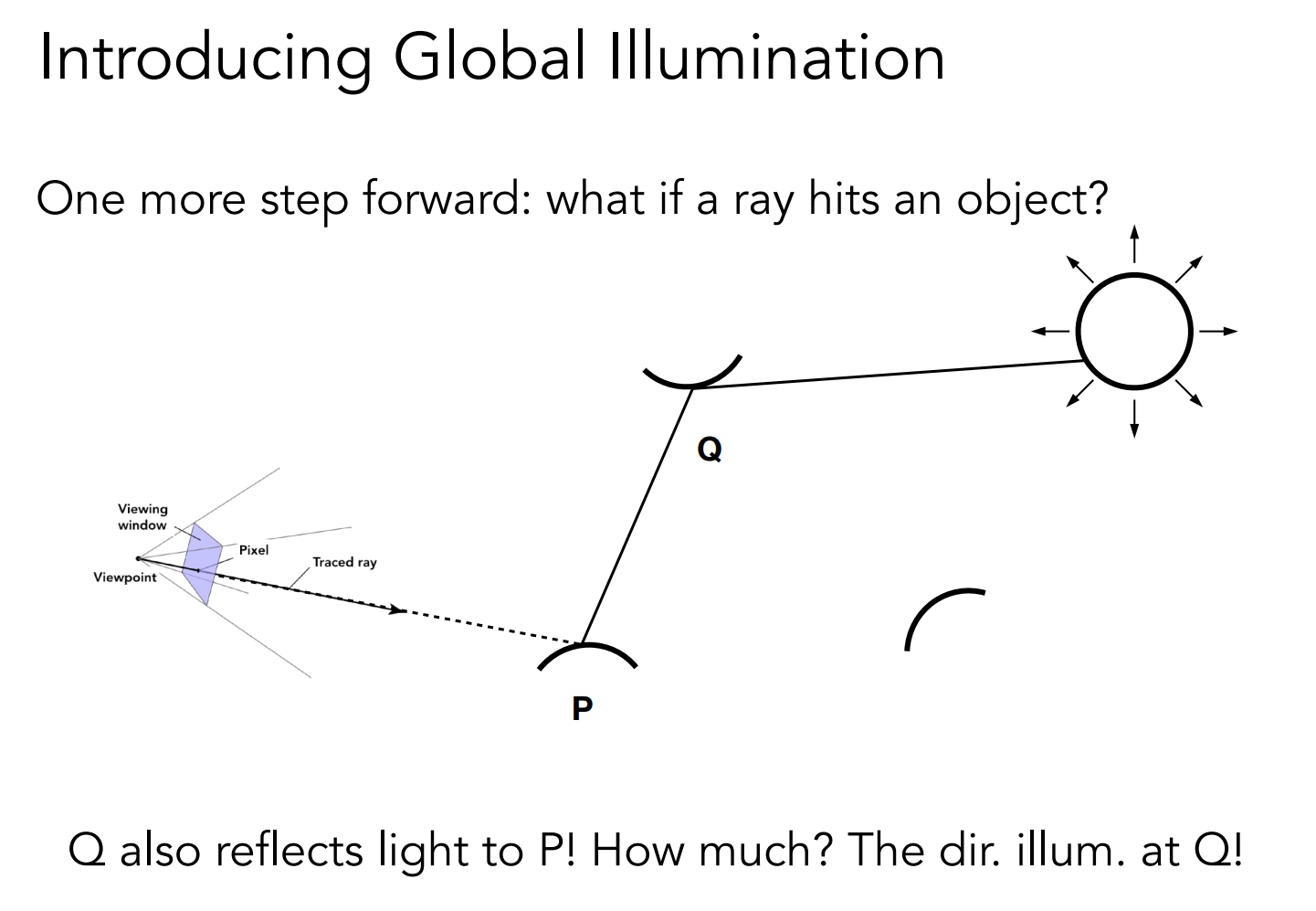
考虑点 P 接收到的来自点 Q 的间接光照，这一结果就相当于对点 Q 进行 Q -> P 方向上出射光 Radiance 的求解，这就变成了递归的求解过程

结合伪代码理解就会很清晰，P 点接受的 Q->P 方向的 radiance，结果就是 shade(q, -wi)。这样就几乎完成了全局光照的求解，但依然会有一些问题。

1. 指数爆炸

   

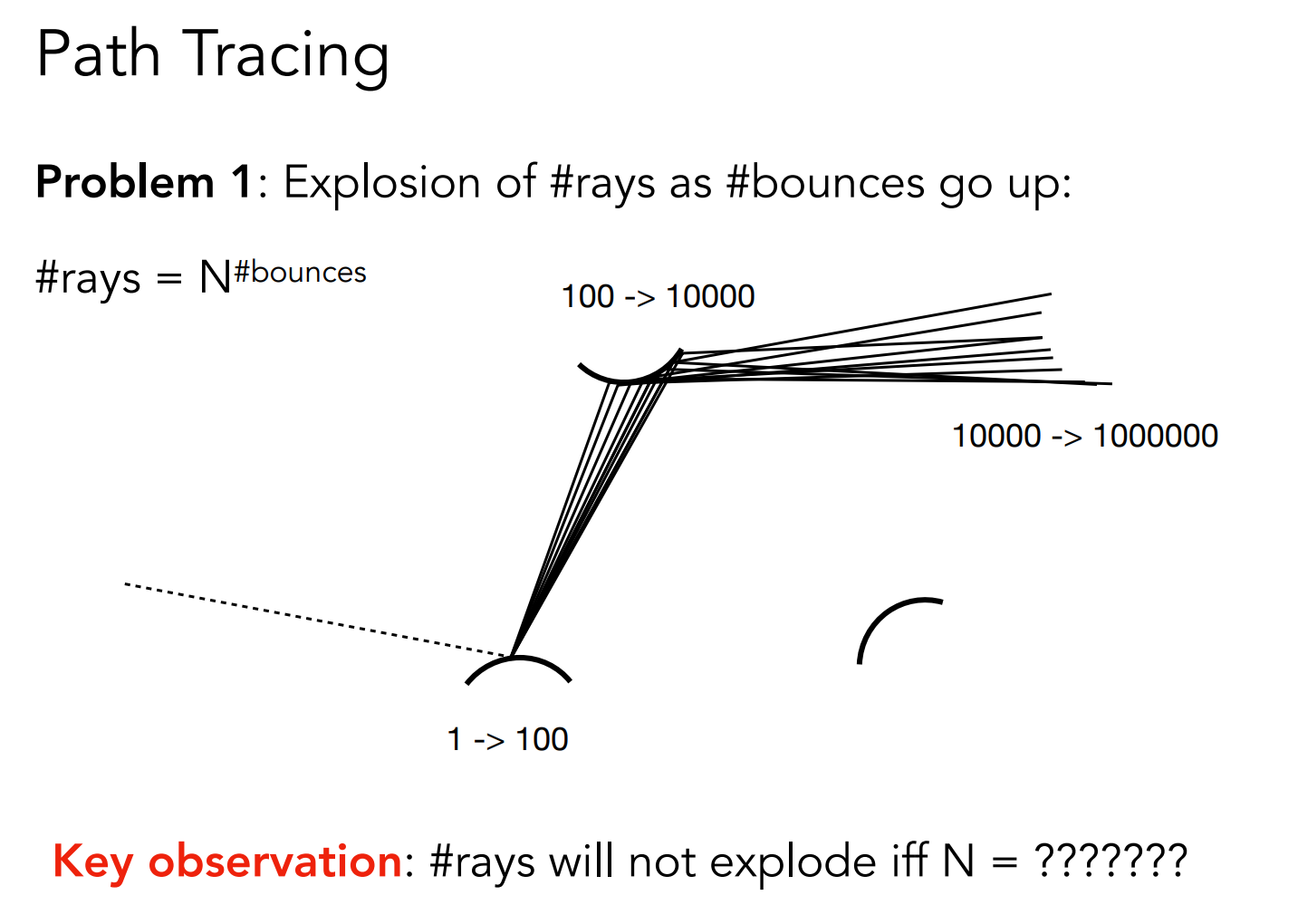
   考虑一个点发射多条光线，显然，在经过了几次弹射后就会出现指数爆炸的问题。

   

   为了避免这个问题，取 $N=1$，即每个点只发出一条光线，这样的方法就被称为路径追踪；当 $N \neq 1$ 时，被称为分布式路径追踪。

2. 递归的终止条件

   

   上述的伪代码是没有终止条件的，因此会一直计算下去；计算机肯定不能处理这种情况，然而现实中光线确实是会一直弹射的。

   

   通过 俄罗斯轮盘赌（RR）的方法，以一个概率 p 决定光线是否继续弹射，同时结果除以 p 保证期望不变。

   

   这样就解决了递归不会结束的问题。

3. 噪声问题

   

   

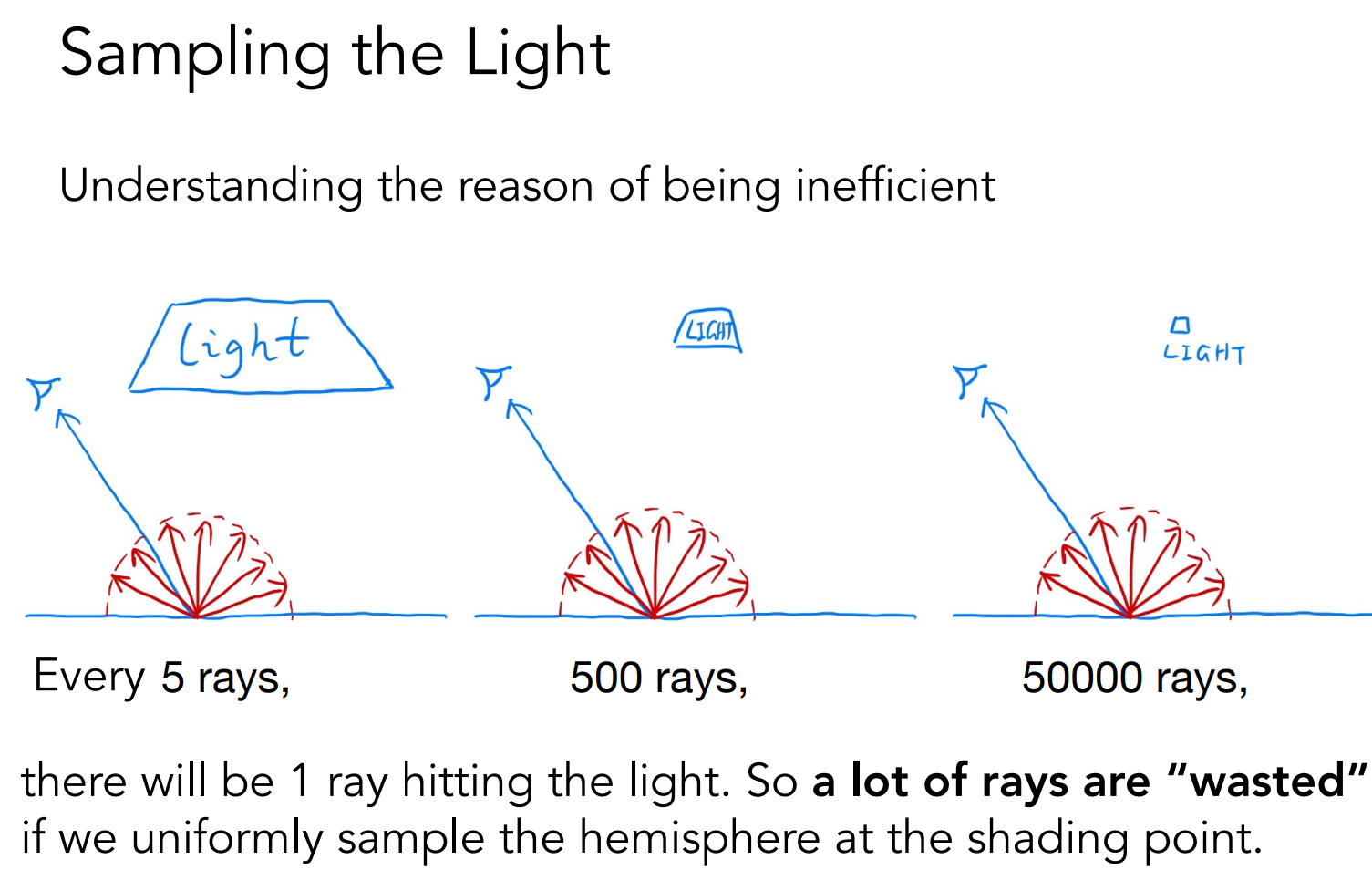
   使用均匀采样的方法会造成很大程度的浪费，有很多光线无法打到光源。

   

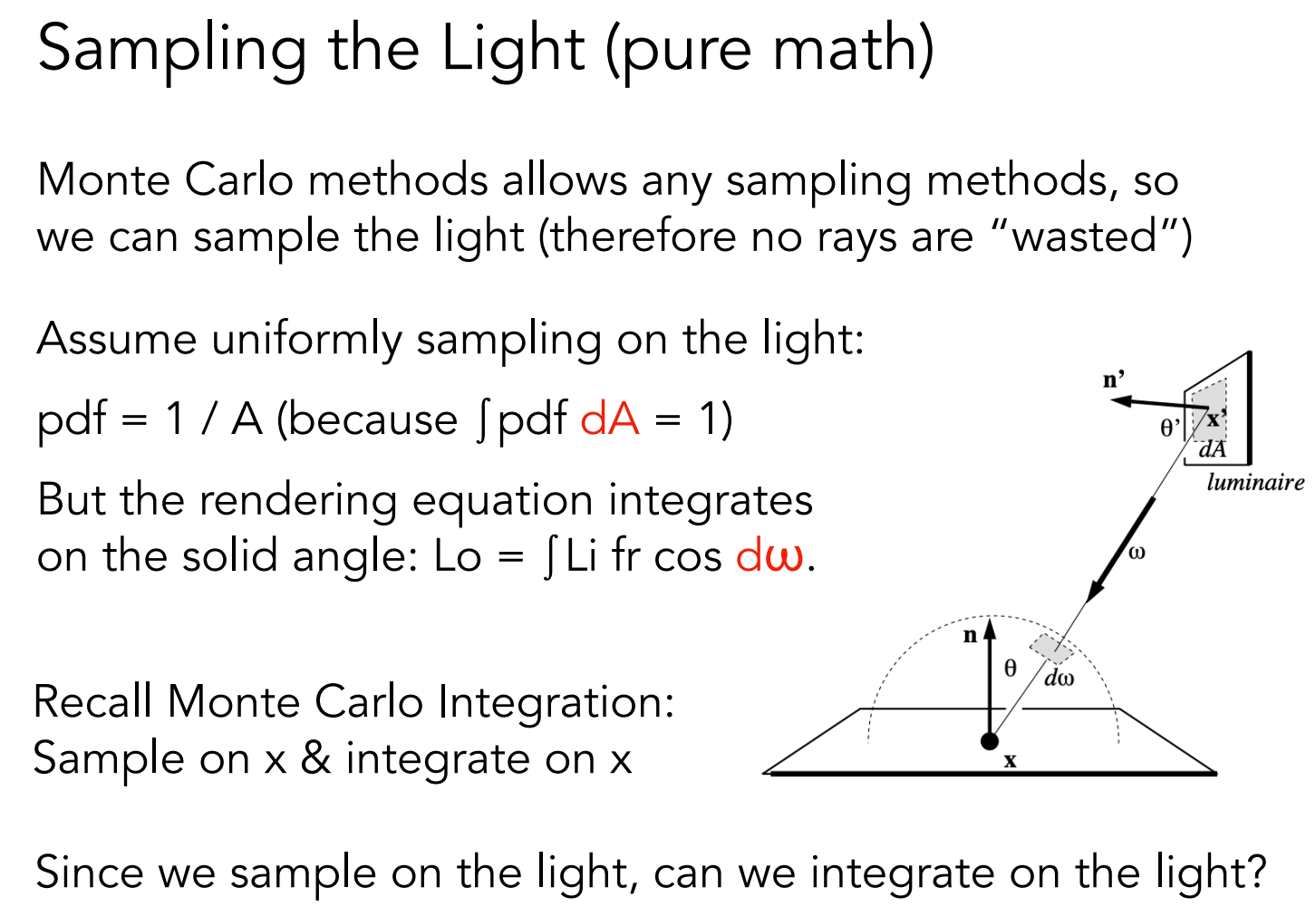
   直接在光源表面进行采样，光线就不会浪费；但是需要注意：蒙特卡洛积分的采样区间与积分区间必须相同。因此需要把积分区间由半球面转换到光源表面。

   

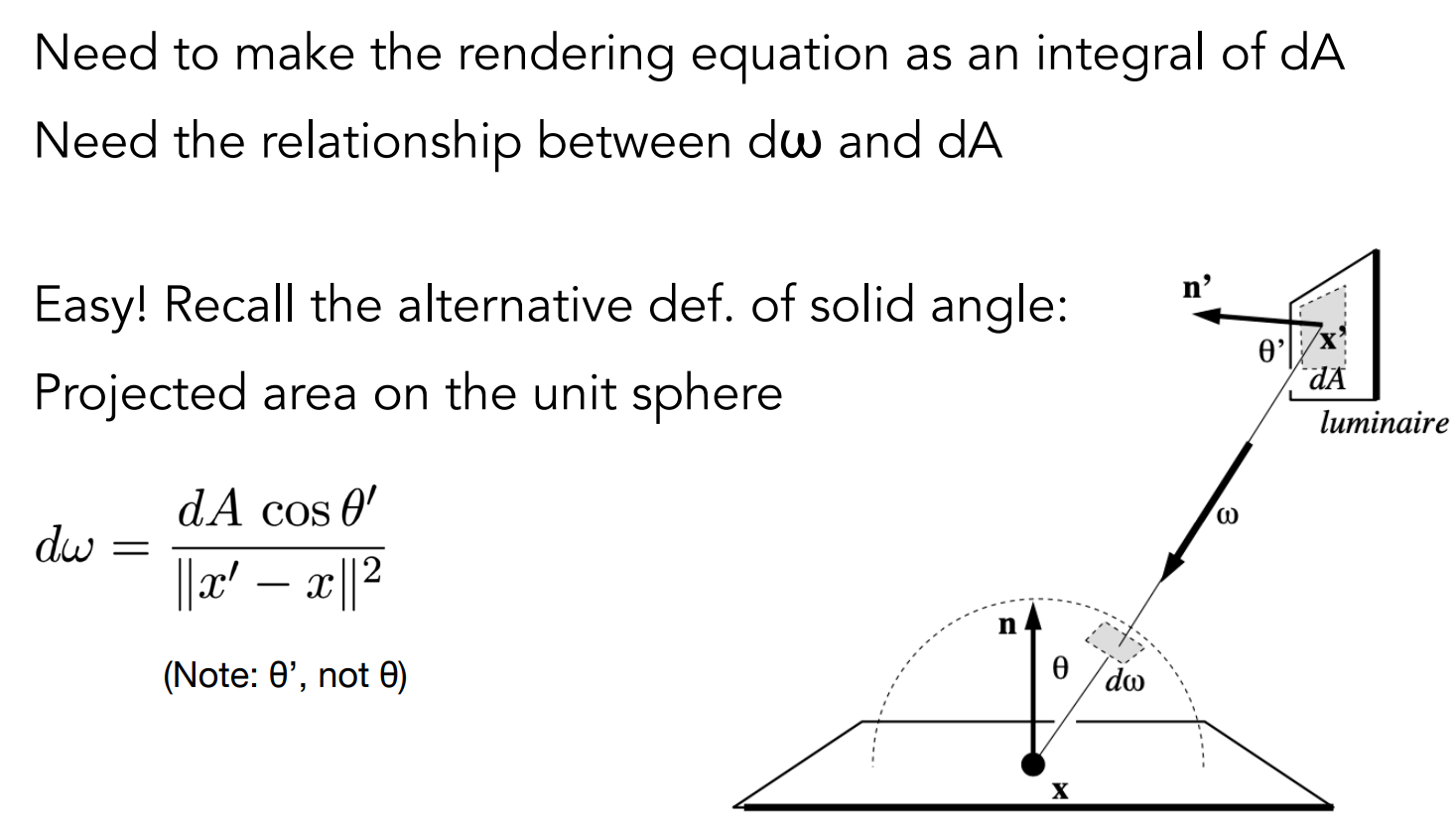
   这样就不会浪费光线了。

   

   

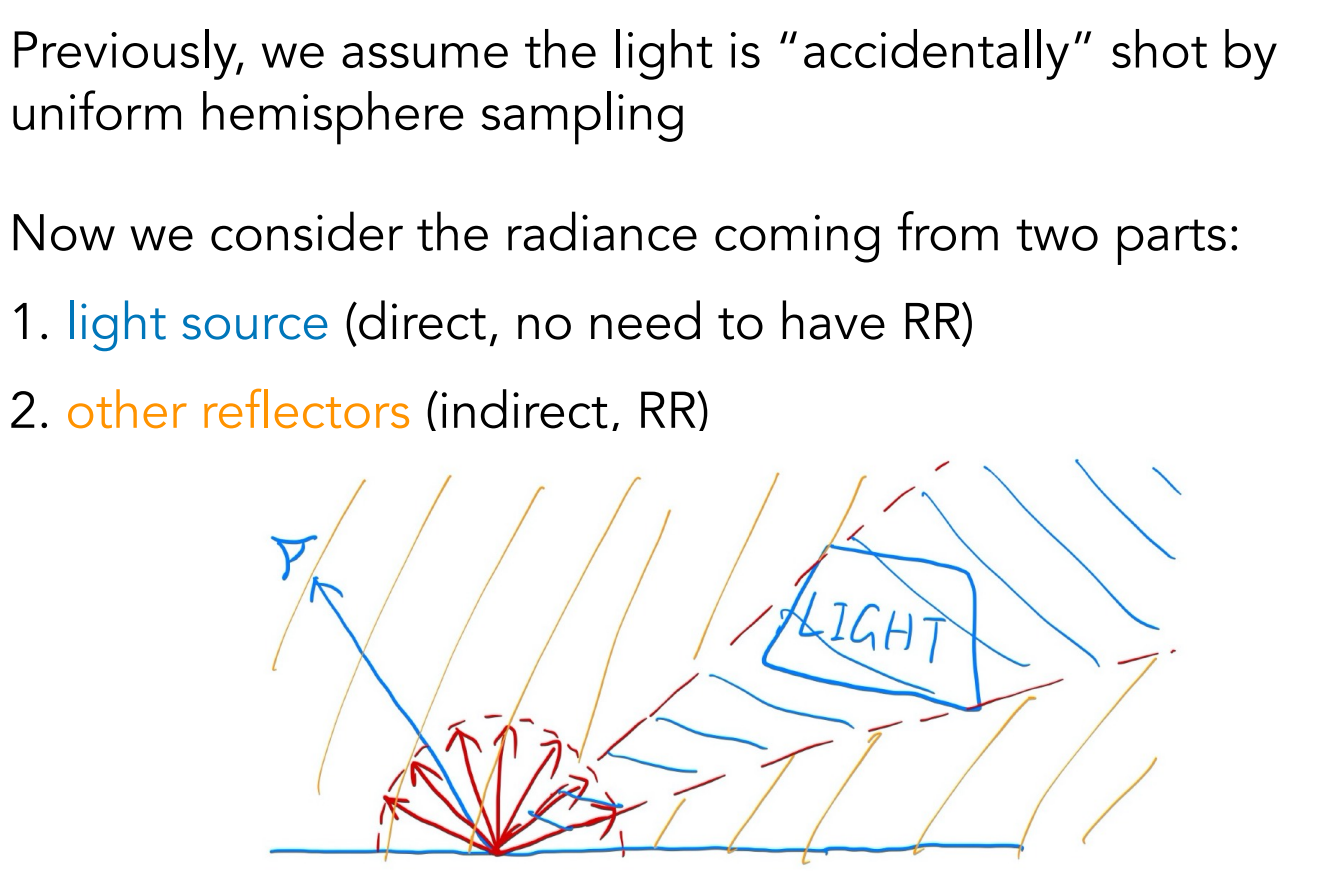
   现在考虑计算，直接光就不需要进行 RR 了，而间接光照则需要继续 RR（以决定是否停止）

   

   最后再判断一下光源与所求的点 p 之间是否被遮挡

至此就完成了 path tracing 求全局光照的过程。

当然，除 path tracing 外还有许多求全局光照的模型，如光子映射等。