前言：场景体素化

UE4的导航使用的是RecastDetour组件，这是一个开源组件，主要支持3D场景的导航网格导出和寻路，或者有一个更流行的名字叫做NavMesh。不管是Unity还是UE都使用了这一套组件。不过UE4对其算法做了不小的修改。

Github上有更为详细的源码、Demo和说明：https://github.com/recastnavigation/recastnavigation

本文使用的UE4源码版本为4.24.3，2020年2月25日的版本。

Recast采用了体素化的方式，来生成导航网格。大致分为三个步骤：

将场景体素化。形成一个多层的体素模型。
将不同层的体素模型划分为可重叠的2D区域。不同层的2D区域不同
沿着边界区域剥离出导航凸多边形。

本文将介绍第一部分，将场景体素化，以及后续的可行走层的过滤。

体素概念介绍

体素的概念和像素类似，将三维空间分成一个个的小格子，如下图所示：

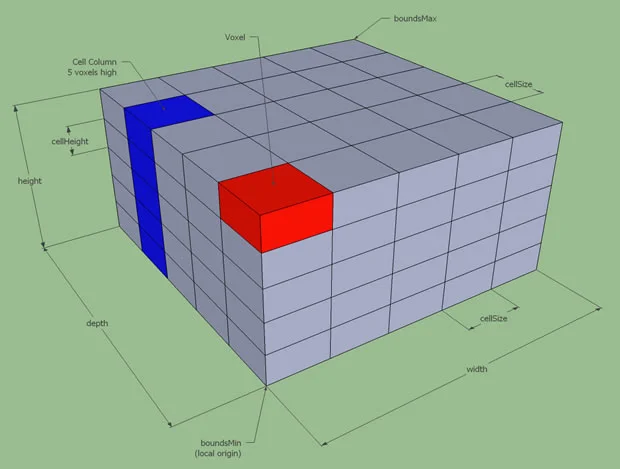
然后是一个概念span：代表某一方向上连续的格子。

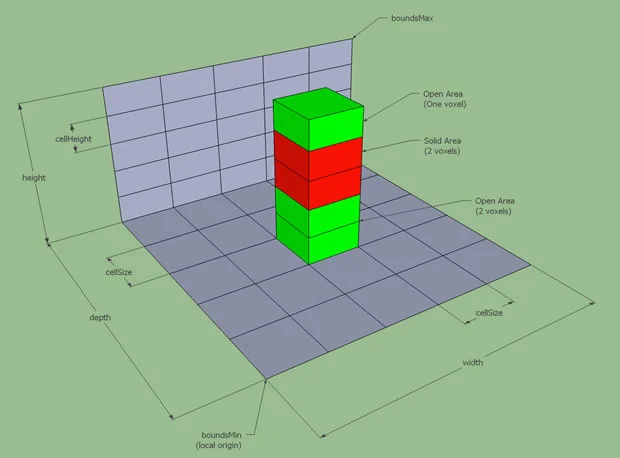
体素化的目的，就是为了将整个场景转换为一个个格子内的体素，并标记每个span的可行走状态。以方便后续做区域划分和寻路。

体素化流程

这一部分会直接使用整个场景所有物件的顶点和三角形数据。大致分为两个步骤：

标记可行走的面。逻辑主要在rcMarkWalkableTrianglesCos()函数中
将网格光栅化。逻辑主要在rcRasterizeTriangles()函数中
过滤可行走表面。逻辑主要在GenerateCompressedLayers()中

标记可行走的面

这部分逻辑主要在rcMarkWalkableTrianglesCos()函数中。

会遍历所有网格的三角形，并计算法线方向。如果发现方向与垂直方向的夹角小于某个配置的值，那么认为这是可行走的。整个函数的实现也很简单。如下：

void rcMarkWalkableTrianglesCos(rcContext* /*ctx*/, const float walkableSlopeCos, const float* verts, int /*nv*/, const int* tris, int nt, unsigned char* areas)
{
	float norm[3];
	for (int i = 0; i < nt; ++i)
	{
		const int* tri = &tris[i*3];
		calcTriNormal(&verts[tri[0]*3], &verts[tri[1]*3], &verts[tri[2]*3], norm);
		// Check if the face is walkable.
		if (norm[1] > walkableSlopeCos)
			areas[i] = RC_WALKABLE_AREA;
	}
}

将网格光栅化

这部分逻辑主要在rcRasterizeTriangles()函数中。更准确说是在rasterizeTri()函数中。

这里使用光栅化这个词，因为Rasterize和渲染管线中的Rasterize是一毛一样的。都是将三角形投影到矩阵（像素或者体素）中。

光栅化的目的，就是找出连续的小格子。不管是连续的开放空间还是连续的密闭空间。光栅化时，也是以三角形为基本单位的。注意这里的坐标系：xz是水平，y是垂直。

这里对着源码简述一下其算法（UE4基本上重写了rasterizeTri()函数。我理解主要为了优化性能。与原始代码相比，增加了更多的直接指针操作，优化了三角形位于一个平面上的情况的性能，减少了函数调用的栈开销。全部用EPIC_ADDITION_USE_NEW_RECAST_RASTERIZER宏包裹。但是不得不吐槽，可读性比Recast源码还差。。）

首先说明一个概念span：代表某一方向上连续的格子。

在上图中，(2,2)这个xz平面的格子上，就有三个span。绿色代表开放空间，红色代表密闭空间。

记录xz平面三角形的投影，是一个AABB的包围盒。

关键源码如下：

// 这是平面上的点，标记三个顶点分别位于哪个格子
int intverts[3][2];

intverts[0][0] = (int)floorf((v0[0] - bmin[0])*ics);
intverts[0][1] = (int)floorf((v0[2] - bmin[2])*ics);
intverts[1][0] = (int)floorf((v1[0] - bmin[0])*ics);
intverts[1][1] = (int)floorf((v1[2] - bmin[2])*ics);
intverts[2][0] = (int)floorf((v2[0] - bmin[0])*ics);
intverts[2][1] = (int)floorf((v2[2] - bmin[2])*ics);

// 这个三角形所投影出来的AABB包围盒，一个矩形
int x0 = intMin(intverts[0][0], intMin(intverts[1][0], intverts[2][0]));
int x1 = intMax(intverts[0][0], intMax(intverts[1][0], intverts[2][0]));
int y0 = intMin(intverts[0][1], intMin(intverts[1][1], intverts[2][1]));
int y1 = intMax(intverts[0][1], intMax(intverts[1][1], intverts[2][1]));

在xz平面上，依次遍历三角形的三条边，三条边经过的格子之间划分成一个FlatSpan。

具体原理是按照z轴遍历，并记录某一格z值上的x的最大值和最小值。其数据结构如下：

struct rcHeightfield
{
    // ...

#if EPIC_ADDITION_USE_NEW_RECAST_RASTERIZER
    rcEdgeHit* EdgeHits; ///< h + 1 bit flags that indicate what edges cross the z cell boundaries
    // 记录了每一个z值上x的最大值和最小值
    rcRowExt* RowExt;		///< h structs that give the current x range for this z row。row代表z，col代表x
    rcTempSpan* tempspans;		///< Heightfield of temp spans (width*height).
#endif
};

核心算法可以概括为：

记录三角形区域的三条边对应的格子，三条边中间的格子是需要去记录竖直方向体素的格子。
记录三角形中间的格子竖直方向连续格子的边界。

注意，这个阶段只是标记连续的实心span。至于span是否可行走，则是在第一个阶段通过判断法线方向与竖直方向的夹角就完成了。实际寻路和后续区域划分用到的都是空心span，会在下一个阶段根据实心span取反生成。

核心算法源代码如下：

// 记录沿着z方向（Col）的连续格子
static inline void addFlatSpanSample(rcHeightfield& hf, const int x, const int y)
{
    // ...
	hf.RowExt[y + 1].MinCol = intMin(hf.RowExt[y + 1].MinCol, x);
	hf.RowExt[y + 1].MaxCol = intMax(hf.RowExt[y + 1].MaxCol, x);
}

static void rasterizeTri(const float* v0, const float* v1, const float* v2, const unsigned char area, rcHeightfield& hf, const float* bmin, const float* bmax, const float cs, const float ics, const float ich, const int flagMergeThr)
{
    // ...
    // 三条边，每条边有两个float3，分别记录方向向量和向量倒数，用来求交点
    float edges[6][3];
    
    // 如果算出来三角形的y方向均位于同一个y内，只需要计算平面的连续区域
	// 分别遍历三个顶点来计算三条边
	for (int basevert = 0; basevert < 3; basevert++)
	{
		int othervert = basevert == 2 ? 0 : basevert + 1;
		int edge = basevert == 0 ? 2 : basevert - 1;

		rcVsub(&edges[edge][0], vertarray[othervert], vertarray[basevert]);
		//rcVnormalize(&edges[edge][0]);
		//预存斜率。这个用来计算交点。
		edges[3 + edge][0] = 1.0f / edges[edge][0];
		edges[3 + edge][1] = 1.0f / edges[edge][1];
		edges[3 + edge][2] = 1.0f / edges[edge][2];
		
		// ...
		
		// 遍历z方向
		if (intverts[basevert][1] != intverts[othervert][1])
		{
			// 如果当前线段不是沿着x轴平行，即两个端点的z值不相等
			
			// 当前所处理的线段edge的z方向最小格子索引
			int edge0 = intMin(intverts[basevert][1], intverts[othervert][1]);
			// 当前所处理的线段edge的z方向最大格子索引
			int edge1 = intMax(intverts[basevert][1], intverts[othervert][1]);
			int loop0 = intMax(edge0 + 1, y0);
			int loop1 = intMin(edge1, y1_edge);

			// 遍历z方向。因为这是三角形的边，所以只要经过的格子都是体素，都需要记录Hits
			unsigned char edgeBits = (edge << 4) | (othervert << 2) | basevert;
			for (int y = loop0; y <= loop1; y++)
			{
				// 这里的Hits存会记录z方向edge和两个线段的两个终点。
				// Hits的长度为2。因为是三角形的三条边，同一个z最多有两条线段，所以这里记录两次
				int HitIndex = !!hf.EdgeHits[y].Hits[0];
				hf.EdgeHits[y].Hits[HitIndex] = edgeBits;
			}
		}
		
		// 遍历x方向，与z方向大致相同
		if (intverts[basevert][0] != intverts[othervert][0])
		{
			// ...
			addFlatSpanSample(hf, x, y);
			addFlatSpanSample(hf, x - 1, y);
			// ...
		}
		
		// 处理垂直方向
		// ...
		for (int y = loop0; y <= loop1; y++, cz += cs)
		{
		    for (int i = 0; i < 2; i++)
			{
				int edge = Hits.Hits[i] >> 4;
				int othervert = (Hits.Hits[i] >> 2) & 3;
				int basevert = Hits.Hits[i] & 3;

				// 求出三角形的两条边在cz平面上的交点
				intersectZ(vertarray[basevert], &edges[edge][0], cz, Inter[i]);
				// 交点的x值
				int x = (int)floorf((Inter[i][0] - bmin[0])*ics);
				xInter[i] = x;
				if (x >= x0 && x <= x1)
				{
					// 这两个交点之间的格子都可以标记
					addSpanSample(hf, x, y, sint);
					addSpanSample(hf, x, y - 1, sint);
				}
			}
			
			// 处理每条边的情况。这里有个分支，如果三条边都在同一个水平面上，代码会简单并且快速很多。这里讨论不在同一水平面上的情况
			if (xInter[0] != xInter[1])
			{
				// 根据斜率计算每个格子上升的ds值
				int left = Inter[1][0] < Inter[0][0];  
				int xloop0 = intMax(xInter[left] + 1, x0);
				int xloop1 = intMin(xInter[1 - left], x1_edge);

				float d = 1.0f / (Inter[1-left][0] - Inter[left][0]);
				float dy = Inter[1-left][1] - Inter[left][1];
				//float ds = dy * d;
				// ds表示相邻两个格子间上升的y值
				float ds = 0.0f;
				float t = rcClamp((float(xloop0)*cs + bmin[0] - Inter[left][0]) * d, 0.0f, 1.0f);
				float sfloat = (Inter[left][1] + t * dy) - bmin[1];
				if (xloop1 - xloop0 > 0)
				{
					float t2 = rcClamp((float(xloop1)*cs + bmin[0] - Inter[left][0]) * d, 0.0f, 1.0f);
					float sfloat2 = (Inter[left][1] + t2 * dy) - bmin[1];
					ds = (sfloat2 - sfloat) / float(xloop1 - xloop0);
				}
				// 在绝对的sint平面上去addSpan
				for (int x = xloop0; x <= xloop1; x++, sfloat += ds)
				{
					short int sint = (short int)rcClamp((int)floorf(sfloat * ich + 0.5f), -32000, 32000);
					addSpanSample(hf, x, y, sint);
					addSpanSample(hf, x - 1, y, sint);
					addSpanSample(hf, x, y - 1, sint);
					addSpanSample(hf, x - 1, y - 1, sint);
				}
			}
		}
		// 最后一个循环，遍历z轴，找到之前记录的每个z值对应的x的最大值和最小值，进行二维遍历。
		for (int y = y0; y <= y1; y++)
		{
			int xloop0 = intMax(hf.RowExt[y + 1].MinCol, x0);
			int xloop1 = intMin(hf.RowExt[y + 1].MaxCol, x1);
			for (int x = xloop0; x <= xloop1; x++)
			{
				// 二维遍历，取到每个格子列的y轴最大值和最小值
				// ...
				addSpan(hf, x, y, smin, smax, area, flagMergeThr);
			}
			// 清理操作
			// ...
		}
	}
}

合并span的核心源码如下：

static void addSpan(rcHeightfield& hf, const int x, const int y, const unsigned short smin, const unsigned short smax, const unsigned char area, const int flagMergeThr)
{
    // ...
    // Cur是当前格子的最底层。这是一个链表，记录了从下往上的span列表
	while (cur)
	{
		// 目的是找到与新span相交的span，然后更新span的数据
		// ...
		{
			// 合并span。即更新span的数据
			if (cur->data.smin < s->data.smin)
				s->data.smin = cur->data.smin;
			if (cur->data.smax > s->data.smax)
				s->data.smax = cur->data.smax;
			
			// 合并可行走标记。只要两者有一个是可行走，那么这个span就是可行走
			if (rcAbs((int)s->data.smax - (int)cur->data.smax) <= flagMergeThr)
				s->data.area = rcMax(s->data.area, cur->data.area);

			// 用新span替换掉当前的span
			// ...
		}
	}
	// ...
}

过滤可行走表面

分为三步：

若一个span标记为可行走，那么位于它上方且高度相差小于walkableClimb的span也应标记为可行走。典型的场景：楼梯台阶。对应的函数为rcFilterLowHangingWalkableObstacles()

核心源码如下：

void rcFilterLowHangingWalkableObstacles(rcContext* ctx, const int walkableClimb, rcHeightfield& solid)
{
    // ...
    for (rcSpan* s = solid.spans[x + y*w]; s; ps = s, s = s->next)
    {
        const bool walkable = s->data.area != RC_NULL_AREA;
        if (!walkable && previousWalkable)
        {
            // 如果当前不可行走，但是其下方span可行走，且两者高度差小于walkableClimb，那么认为当前可行走
            if (rcAbs((int)s->data.smax - (int)ps->data.smax) <= walkableClimb)
                s->data.area = previousArea;
        }
        previousWalkable = walkable;
        previousArea = s->data.area;
    }
    // ...
}

如果一个span和其邻居之间的高度差过大，超过了walkableClimb，那么认为自己在陡坡上，不可达。另外如果其邻居之间的高度差过大，也认为不可达。对应的函数为rcFilterLedgeSpans()

核心源码如下：

void rcFilterLedgeSpans(rcContext* ctx, const int walkableHeight, const int walkableClimb, rcHeightfield& solid)
{
    // 三维来遍历每个span...
    {
        // 当前span的最顶部
        const int bot = (int)(s->data.smax);
        // 其上方span的最底部
        const int top = s->next ? (int)(s->next->data.smin) : MAX_HEIGHT;
        
        // 表示自己和邻居之间的高度差
        int minh = MAX_HEIGHT;

        // 可达邻居的最小高度
        int asmin = s->data.smax;
        // 可达邻居的最大高度
        int asmax = s->data.smax;

        for (int dir = 0; dir < 4; ++dir)
        {
            // 遍历四个邻居
            // ...
            rcSpan* ns = solid.spans[dx + dy*w];
            // 从可以攀爬的-walkableClimb开始
            int nbot = -walkableClimb;
            // 邻居span的最底部
            int ntop = ns ? (int)ns->data.smin : MAX_HEIGHT;
            // 判断邻居和自己的缝隙的高度差是否容许一个人通过
            if (rcMin(top,ntop) - rcMax(bot,nbot) > walkableHeight)
                minh = rcMin(minh, nbot - bot);
            
            for (ns = solid.spans[dx + dy*w]; ns; ns = ns->next)
            {
                // 遍历邻居竖直方向的所有span
                nbot = (int)ns->data.smax;
                ntop = ns->next ? (int)ns->next->data.smin : MAX_HEIGHT;
                if (rcMin(top,ntop) - rcMax(bot,nbot) > walkableHeight)
                {
                    // 和邻居的地面的高度差
                    minh = rcMin(minh, nbot - bot);
                
                    // Find min/max accessible neighbour height. 
                    if (rcAbs(nbot - bot) <= walkableClimb)
                    {
                        // 如果高度差可以攀爬，认为该邻居可达，那么记录可达邻居的最小高度asmin和最大高度asmax
                        if (nbot < asmin) asmin = nbot;
                        if (nbot > asmax) asmax = nbot;
                    }
                    
                }
            }
        }
        
        // 自己和邻居之间的地面的高度差。如果过大，那么认为不可达
        if (minh < -walkableClimb)
            s->data.area = RC_NULL_AREA;
            
        // 比较可达邻居之间的高度差。如果不同邻居之间高度相差过大，则认为在陡坡上，自己也不可达
        if ((asmax - asmin) > walkableClimb)
        {
            s->data.area = RC_NULL_AREA;
        }
    }
    // ...
}

如果某个span可行走，但是其上方有不可行走的障碍物，也认为不可行走。实现函数为rcFilterWalkableLowHeightSpans()。源码也非常非常简单。

for (int y = 0; y < h; ++y)
{
    for (int x = 0; x < w; ++x)
    {
        for (rcSpan* s = solid.spans[x + y*w]; s; s = s->next)
        {
            const int bot = (int)(s->data.smax);
            const int top = s->next ? (int)(s->next->data.smin) : MAX_HEIGHT;
            if ((top - bot) <= walkableHeight)
                s->data.area = RC_NULL_AREA;
        }
    }
}

总结

至此，从源码层面分析了UE4是如何将场景体素化的。总体来看，并没有使用大量射线或者三角函数，而是简单的利用遍历、大小值比较、比例换算，以及基本的指针操作来省去函数调用压栈的开销，甚至为了优化计算速度使用乘法来代替除法。之前我们的项目组，体素方案是使用从上往下打射线的方式来实现的，用于线下制作没问题，代码也简单一些，但是速度比起来就差很多了。

下一篇将会讲述区域划分的流程。