UE 补完计划(四) 导航系统-4
前言:区域划分算法–Watershed与Monotone
UE4的导航使用的是RecastDetour组件,这是一个开源组件,主要支持3D场景的导航网格导出和寻路,或者有一个更流行的名字叫做NavMesh。不管是Unity还是UE都使用了这一套组件。
Github上有更为详细的源码、Demo和说明:https://github.com/recastnavigation/recastnavigation
本文使用的UE4源码版本为4.24.3,2020年2月25日的版本。
Recast采用了体素化的方式,来生成导航网格。大致分为三个步骤:
将场景体素化。形成一个多层的体素模型。
将不同层的体素模型划分为可重叠的2D区域。不同层的2D区域不同
沿着边界区域剥离出导航凸多边形。
在上一篇文章,讲述了整个区域生成的过程,并简单介绍了Monotone区域划分算法。这一篇会从理论说起,并深入源码层面,详细解读Watershed算法的实现。
WaterShed 算法
Watershed算法中文名称叫做分水岭算法,是一种利用已有的深度图划分区域的算法。在图像处理上也经常用于利用灰度值划分一张图片上的不同色块(想象一下Photoshop的魔棒工具)
为了更好理解这个算法,这里将原理和实现源码分开讲述。
原理
我们将不可达的地方看做山脉,并进行标记。将可达区域按照离山脉的远近去划分高度。并规定:离山脉越远的地方,地势越低。
假设我们规定,沿着x轴或者z轴的高度差为2,斜向的高度差为3。
原始的场景图如下(0表示不可行走的区域):
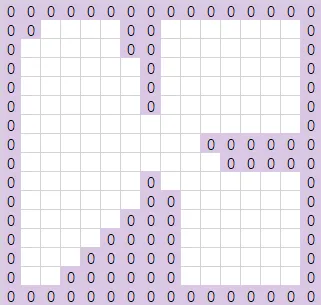
-
我们做一次深度采样,严格遵循离山脉越远的地方,地势越低的原则,可以得到的高度图如下:
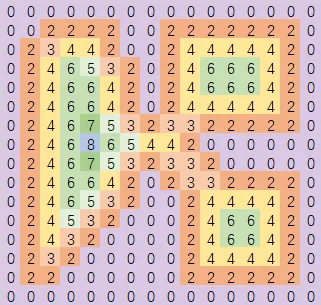
图中的数字表示其深度。所以严格来说,这是一张“深度图”。
(在Recast的处理中,这里还有一步Blur的操作)
-
为场景中每个最低的区域分配一个区域id。在图中,最低区域的level是8。在UE4的算法中,距离值每次迭代会减2。这里我们严格按照UE4的算法,依次进行迭代灌水:
第一次灌水,处理距离为7和8的格子:

第二次灌水,处理距离为5和6的格子:

第三次灌水,处理距离为3和4的格子:

第四次灌水,处理距离为2的格子:

四次灌水之后,当前的场景就处理完毕了。以上图例是严格按照UE4的算法来绘制的。接下来会从源码层面分析代码。
实现流程
构建高度图
根据每个span的可行走信息,来构造出dist矩阵。存储每个区域距离四周不可行走区域的最近距离。
核心函数在calculateDistanceField()函数中。主要由三个pass构成:
-
Pass1:遍历所有span,找到和邻居span不连通的,这就是整个地形图的边界。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21// 算法和rcErodeWalkableArea函数类似。同样是寻找边界。不同的是ErodeWalkableArea只是为了标记处不可走以及和不可走相邻的区域,而这里则是为了标记处和周围不一样的区域
// 这个pass过后,找到了所有边界点。边界点的src均为0,非边界点的src均为0xffff。
// ...遍历所有span
const rcCompactSpan& s = chf.spans[i];
const unsigned char area = chf.areas[i];
int nc = 0;
for (int dir = 0; dir < 4; ++dir)
{
if (rcGetCon(s, dir) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(dir);
const int ay = y + rcGetDirOffsetY(dir);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, dir);
// 注意这个判断,即使两边都等于0,nc也会增加
if (area == chf.areas[ai])
nc++;
}
}
if (nc != 4)
src[i] = 0; -
Pass2:从左下方向开始收拢,计算左下的四个方向,递归计算离边界的距离。其中沿轴方向距离相差2,斜方向距离相差3。
1
2
3
4
5
6
7
8
9
10
11
12
13
14// ...遍历所有span
if (rcGetCon(s, 0) != RC_NOT_CONNECTED)
{
// (-1,0)
// 左侧
const int ax = x + rcGetDirOffsetX(0);
const int ay = y + rcGetDirOffsetY(0);
const int ai = (int)chf.cells[ax+ay*w].index + rcGetCon(s, 0);
const rcCompactSpan& as = chf.spans[ai];
if (src[ai]+2 < src[i])
src[i] = src[ai]+2;
//...其它方向算法类似
} -
Pass3:从右上向左下收拢,计算右上的四个方向。算法和Pass2一致。
-
在计算完高度图之后,做一次blur,让高度图更加平滑。核心函数在
boxBlur()中。算法很简单,就是取周围八个点的dist值,加上自己累加起来,然后平均之后四舍五入。1
2// d为九个格子累加之后的值
dst[i] = (unsigned short)((d+5)/9);
向地形图灌水(Watershed流程)
核心代码在rcGatherRegionsNoFilter()中。
-
初始化
在生成地形深度图的过程中,会记录最大深度。整个灌水的迭代会从最大深度开始。有一点需要注意的是,由于整个深度图,沿轴方向距离相差2,斜方向距离相差3,意味着场景中的深度有可能为奇数也有可能为偶数。这里默认将初始深度取偶数处理。
1
2// 最终结果是如果maxDistance是奇数,那么level=maxDistance+1,如果是偶数,那么level=maxDistance。不管怎样level会是偶数
unsigned short level = (chf.maxDistance+1) & ~1;算法也使用了广度遍历+深度遍历的结合。一般来说广度遍历会有更好的形状,但是速度偏慢。深度遍历会生成更尖锐的形状,不过速度快。使用一个
expandIters变量来控制广度遍历的最大迭代次数。默认值为8。1
2
3
4
5
6// TODO: Figure better formula, expandIters defines how much the
// watershed "overflows" and simplifies the regions. Tying it to
// agent radius was usually good indication how greedy it could be.
// const int expandIters = 4 + walkableRadius * 2;
// 在expandIters内的迭代使用广度遍历。expandIters之外的迭代使用深度遍历。一般来说广度遍历会有更好的形状,但是速度偏慢。
const int expandIters = 8;在初始化时,会根据
bordersize来设立边界。边界以内bordersize以内的格子都是不可走的。1
2
3
4
5
6
7
8
9
10
11
12
13if (borderSize > 0)
{
// Make sure border will not overflow.
const int bw = rcMin(w, borderSize);
const int bh = rcMin(h, borderSize);
// 将靠近边界的bordersize区域设置为不可寻路
paintRectRegion(0, bw, 0, h, regionId|RC_BORDER_REG, chf, srcReg); regionId++;
paintRectRegion(w-bw, w, 0, h, regionId|RC_BORDER_REG, chf, srcReg); regionId++;
paintRectRegion(0, w, 0, bh, regionId|RC_BORDER_REG, chf, srcReg); regionId++;
paintRectRegion(0, w, h-bh, h, regionId|RC_BORDER_REG, chf, srcReg); regionId++;
chf.borderSize = borderSize;
} -
外层控制逻辑
整个外层代码很简单:一定次数以内广度遍历。超过次数深度遍历。(省去了无关紧要的代码)。
这里简单说一下算法中关于广度遍历和深度遍历的权衡:
一次广度遍历,会完全遍历一次格子,会将当前的区域向四周扩散一次。默认的广度遍历最大次数为8,相当于经过广度遍历的过程,已经将区域向外扩展了8个格子,一般来说基本区域已经扩展成型了。一般来说剩下的未扩展的区域也已经是比较狭长的区域,用贪心思想去深度遍历的效果也不会太差。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38// level的初始值会设为maxDistance
while (level > 0)
{
// 在一开始就将level减2
level = level >= 2 ? level-2 : 0;
// 扩展一次当前level的区域。使用广度遍历
if (expandRegions(expandIters, level, chf, srcReg, srcDist, dstReg, dstDist, stack) != srcReg)
{
rcSwap(srcReg, dstReg);
rcSwap(srcDist, dstDist);
}
// Mark new regions with IDs.
for (int y = 0; y < h; ++y)
{
for (int x = 0; x < w; ++x)
{
const rcCompactCell& c = chf.cells[x+y*w];
for (int i = (int)c.index, ni = (int)(c.index+c.count); i < ni; ++i)
{
if (chf.dist[i] < level || srcReg[i] != 0 || chf.areas[i] == RC_NULL_AREA)
continue;
// 一般来说,如果expandRegions中迭代次数过多,超过expandIters数量限制,那么会对剩下的满足要求的区域使用floodRegions进行深度遍历。
// flood的过程类似于深度遍历。一次性找出所有满足level要求的区域。如果有两个区域,区域a和区域b拥有相邻联通且level相同的邻居,那么这些邻居会全部划分给先遍历到的区域a。
if (floodRegion(x, y, i, level, regionId, chf, srcReg, srcDist, stack))
regionId++;
}
}
}
}
// Expand current regions until no empty connected cells found.
if (expandRegions(expandIters*8, 0, chf, srcReg, srcDist, dstReg, dstDist, stack) != srcReg)
{
rcSwap(srcReg, dstReg);
rcSwap(srcDist, dstDist);
} -
广度遍历(expandRegions)
核心代码在expandRegions()函数中。
整个函数的算法可以概括为:
- 遍历所有距离大于等于
level的格子,寻找已标记的邻居节点,标记自身到dstReg中。如果没有任何已标记的邻居节点的格子,会留到下一次遍历 - 交换
srcReg和dstReg,继续1步骤 - 当所有格子都遍历完成,或者迭代次数超过上限,中止循环
这里把整个函数的代码全部列出来:
1 | /* |
- 深度遍历(floodRegions)
经过了之前广度遍历的过程,一般来说基本区域已经扩展成型了。一般来说剩下的未扩展的区域也已经是比较狭长的区域,用贪心思想去深度遍历的效果也不会太差,而且速度更快。
核心代码在floodRegions()中。基本算法与expandRegions()类似,区别就是当找出满足要求的邻居节点时,将邻居节点直接入栈加入当前循环。
1 | /** |
至此,就划分完成了所有的region。我们再来看一下划分完毕的区域:

Monotone 算法
原理
Monotone算法如同其名字一样,一次二维遍历就能划分出区域。这是一种效率非常非常高的区域划分算法。我们依然用相同的区域来讲解Monotone算法的过程:
原始区域如下:

Monotone的关键是“单调”。假设x轴正方向是向右,y轴正方向是向上,我们从-x往x方向,以及-y往y方向来遍历。我们定义某一行的某个连续格子区域成为一个sweepSpan。
-
先遍历第一行,固定y=0,遍历x。连续的格子分配相同的id:
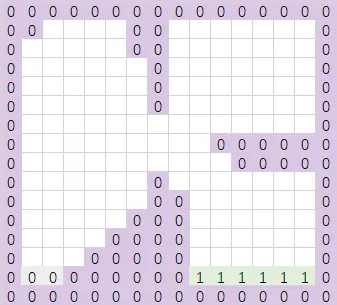
-
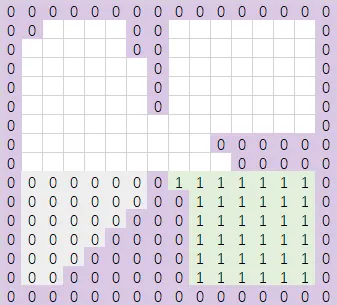
继续遍历第二行,如果某个
sweepSpan的-y方向有且只有一个sweepSpan,且这两个sweepSpan均没有与其它sweepSpan相邻,那么合并这两个sweepSpan。直接将其-y方向的sweepSpan的区域id设为自己的区域id。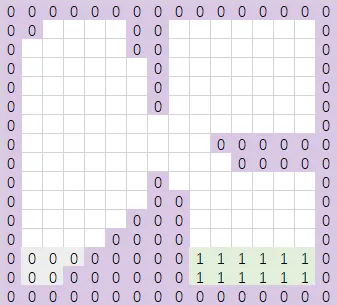
同理,可得:
-
如果某个
sweepSpan的-y方向有两个及两个以上的sweepSpan,那么新创建一个region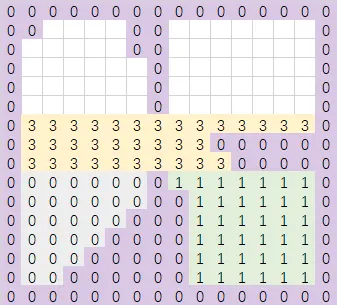
-
如果本行有两个或两个以上的
sweepSpan在-y方向共享同一个sweepSpan邻居,那么这两个sweepSpan都需要新创建一个region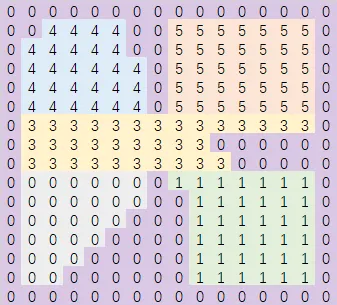
最终划分的区域就如图所示。
实现流程
实际上的算法和流程都已经在上一部分较详细的说明了。下面从源码层面来看看它是如何实现这个算法的。整个核心代码全都在CollectLayerRegionsMonotone()函数中。
整个算法比Watershed简单很多,代码也要简单很多。
核心思想是遍历所有span,从y=0,x=0开始进行二维遍历。让新regionId尽量和左侧和下侧的保持一致
-
从左向右遍历,记录左侧的sweepId,自身的regionId和左侧的regionId保持一致
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31// -x
// -x方向如果是联通的,记录其regionId
if (rcGetCon(s, 0) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(0);
const int ay = y + rcGetDirOffsetY(0);
const int ai = (int)chf.cells[ax + ay*w].index + rcGetCon(s, 0);
if (chf.areas[ai] != RC_NULL_AREA && srcReg[ai] != 0xffff)
sid = srcReg[ai];
}
// 如果-x方向不连通,那么开始标记一个新区域
if (sid == 0xffff)
{
sid = sweepId++;
if (sid < MaxSweeps)
{
sweeps[sid].nei = 0xffff;
sweeps[sid].ns = 0;
}
else
{
ctx->log(RC_LOG_ERROR, "CollectLayerRegionsMonotone: Layer split is too complex, skipping tile! x:%d y:%d spansTotal:%d spansCurrent:%d spansMax:%d", x, y, chf.spanCount, c.count, MaxSpanCount);
return false;
}
}
// ...处理-y方向
srcReg[i] = sid; -
遍历过程中,查找下方(-y方向)的格子。统计自身
sweepSpan和下方相连通的格子数量,以及下方sweepSpan与自己这行相连通的格子数量。如果两者相等,那么说明这两个sweepSpan之间只有一处联通,可以合并。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44// -y
if (rcGetCon(s, 3) != RC_NOT_CONNECTED)
{
const int ax = x + rcGetDirOffsetX(3);
const int ay = y + rcGetDirOffsetY(3);
const int ai = (int)chf.cells[ax + ay*w].index + rcGetCon(s, 3);
// 扫描时是从左向右从下向上,因此可以保证左边和下方一定已经扫描过
// nr表示上方的sweepspanid
const unsigned short nr = srcReg[ai];
if (nr != 0xffff)
{
// sid是左侧方向的邻居。如果左侧刚开始标记一个新区域,或者左侧和自身在同一个区域,将自身加入到这个rcLayerSweepSpan中
if (sweeps[sid].ns == 0)
sweeps[sid].nei = nr;
if (sweeps[sid].nei == nr)
{
sweeps[sid].ns++;
prev[nr]++; // 统计下方的区域包含的格子数
}
else
{
// 下方的regionid与自身已经记录的regionid不等,说明有超过1个的sweepSpan
// 如果上方有超过1个的sweepSpan,那么将nei设为0xffff
sweeps[sid].nei = 0xffff;
}
}
}
//...
for (int i = 0; i < sweepId; ++i)
{
// 遍历本行每一个连续的sweepSpan,如果上方只有一个连续的sweepSpan区域,那么合并这两个sweepSpan
if (sweeps[i].nei != 0xffff && prev[sweeps[i].nei] == sweeps[i].ns)
{
sweeps[i].id = sweeps[i].nei;
}
else
{
sweeps[i].id = regId++;
}
} -
重新分配regId
1
2
3
4
5
6
7
8
9
10// 之前srcReg记录的是sweepId,现在重新记录为regId
for (int x = borderSize; x < w - borderSize; ++x)
{
const rcCompactCell& c = chf.cells[x + y*w];
for (int i = (int)c.index, ni = (int)(c.index + c.count); i < ni; ++i)
{
if (srcReg[i] != 0xffff)
srcReg[i] = sweeps[srcReg[i]].id;
}
}
两种算法比较
形状
我们直接来看两种算法最终得到的区域形状。
Watershed:

Monotone:

这幅图也非常直观展示了两者形状的区别。Watershed算法模拟水位升高,更加自然。Monotone的形状则更加平直狭长。
性能
分析性能时,我们将纵向全部舍去,就单单比较平面的性能。
-
Watershed:
时间复杂度与场景中的最大深度相关。
-
首先需要构建深度图(
O(3*n^2)) -
假设最大深度为
l。在单次深度循环中,首先需要找到满足当前深度要求的格子(O(n^2)),假设满足要求的格子数为m,那么单次循环的复杂度为O(n^2 + 4*m)。总时间复杂度为O(l*(n^2+4*m))
总时间复杂度为
O((l+3)*n^2+4*m*l),大致相当于O(l*n^2),其中l为最大深度。 -
-
Monotone:
这个时间复杂度计算起来简单多了,就是二维遍历次数+每一行的sweep区域数目。即
O(n^2+n*m+n^2),其中m是每一行的sweep区域数目,大致相当于O(n^2)。
结论:
Monotone有明显的性能优势,但是分割出来的形状并不自然。Watershed性能稍差,但是分割出来的形状更加自然,更加贴近人工划分的形状。
小结
这一篇着重分析了UE4使用的两种区域划分算法:Watershed和Monotone,并从源码层面完全分析了其代码实现过程。总体来看:Monotone有明显的性能优势,但是分割出来的形状并不自然。Watershed性能稍差,但是分割出来的形状更加自然,更加贴近人工划分的形状。UE4默认使用的算法是Watershed。
下一篇将会讲述Detour模块如何预处理数据来支持3D寻路,以及A*算法。



