2022年8月22日那天起，多了一个行业，叫 AIGC。

Stable Diffusion 的发布的确颠覆了很多人的认知：“用一段文字生成图片”。这是多么反人类的操作。

但我看到的，其实不是文生图的技术，这东西早就有了，Google 的 Imagen 已经达到了真实照片级别、DALL·E 都出 2 了… 让我感到与之前 AI 不同的地方是，这东西的效果已经跨越了 Demo 的阶段。不知道大家是不是都有这种体验：AI 主要是做 Demo 牛逼，实际跑起来还是堆人或者堆代码。而 Stable Diffusion 让我第一次有了种感觉，这次，兴许真能用。

而让我再一次有这个感觉的，当然就是 ChatGPT 和 Llama 2 了。而最近出的 Sora 看 Demo 的话确实也很厉害，只是除了让互联网多出更多垃圾以外，我个人觉得这个场景也没什么太多意义了。但本文只讨论技术。如果只看技术的话，我是指，只看 OpenAI 说了又好像没说但不得不说确实还是说了点的技术细节的话，似乎可以理解为一个 Stable Diffusion 加了几层 Temporal Attention、UNet 也换成 Attention、又把 KL-reg 的 VAE 换成了针对视频的 VQ-VAE。当然以 OpenAI 的一贯作风估计依旧是省略了很多 “Secret Sauce”，真正技术细节就不得而知了。

Temporal Attention 本文就不多浪费口舌了，它本身其实是个很简单的概念，就是把普通的 Attention 在时间和空间维度上换一下位置，我见过的一般都是作为残差直接加在 Spatial Attention 结果之后，但实际使用时想必也有很多复杂情况。而 UNet 换 Attention 也就是所谓 DiT 这种事情也是老生常谈了，就连 SD3 自己也都开启 Attention 真香模式了。

那，就只留给了我们一个话题：VAE。

什么是VAE？

如果让你教会一个 5 岁小孩子写字，你会怎么教？

你可能会想先从最简单的“一”、“二”、“三”开始教。但你提起笔又想了一下，其实汉字“一”并不好写：

image.png

你沉默了，但很快灵机一动。

那么教写阿拉伯数字总行了吧，“1”、“2”、“3”、“4”、“5” 没那么多规矩，能看懂就行。于是你写下了一个“1”，让孩子照着画，孩子很聪明，也画出来了一个 “1”；你又写下了一个“2”，孩子又画出了一个“2”… 很快，孩子学会了照着画出十个数字。在孩子的世界里，他看到了一个数字的同时，脑子里某些神经连接被激活，在大脑内形成了某种信息，我们可以把这个过程叫作 Encoder；然后大脑拿着这些信息去操控手部神经和肌肉，孩子又重新画出了一个数字，这其实是个 Decoder。

在这个过程中，我们没有告诉孩子应该要在大脑里如何运作或者形成什么样的脑内信息，甚至我们自己都根本不知道大脑是如何运作的，只要能够最终 “decode” 出来一个重新画得比较像的数字即可，整个过程是自动学习的，这就已经是个 Auto Encoder 了。

这个时候你又写下了个“1”，孩子却照着画出来个“7”。你很生气，准备揍他一顿，但你又想到这也不能完全赖孩子，毕竟“1”和“7”确实有点像，这反倒是说明孩子并没有完全在照抄，很可能大脑内对于图形已经有了自己的理解，只是在大脑中的某种多维超空间中处理信息时，“1”和“7”的超空间距离比较近，其实是件好事。如果孩子是把“1”和“5”搞混了，那才说明可能孩子只是在单纯地照抄，并不理解不同图形的差异。而我们接下来要推导的 VAE，也就是 Variational Auto Encoder，就可以避免这种情况出现，让相近的图形在 “encode” 之后的空间内依然保持相近，甚至还会保证该空间连续性，不让孩子画出一些莫名其妙的东西出来。

训练一个平平无奇的 AE 吧

AE，即 Autoencoder，概念本身很简单，简单到 Lightning 的 Quickstart 三十几行代码直接用它作为例子。那么，我们就做我们最擅长的事，把人家的代码复制粘贴下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
import os
from torch import optim, nn, utils, Tensor
from torchvision.datasets import MNIST
from torchvision.transforms import ToTensor
import lightning as L

# define any number of nn.Modules (or use your current ones)
# 我把这里的 `3` 都改成了 `2`，因为我们想要把中间这个维度可视化出来，`2` 维的方便看 
encoder = nn.Sequential(nn.Linear(28 * 28, 64), nn.ReLU(), nn.Linear(64, 2))
decoder = nn.Sequential(nn.Linear(2, 64), nn.ReLU(), nn.Linear(64, 28 * 28))


# define the LightningModule
class LitAutoEncoder(L.LightningModule):
    def __init__(self, encoder, decoder):
        super().__init__()
        self.encoder = encoder
        self.decoder = decoder

    def training_step(self, batch, batch_idx):
        # training_step defines the train loop.
        # it is independent of forward
        x, y = batch
        x = x.view(x.size(0), -1)
        z = self.encoder(x)
        x_hat = self.decoder(z)
        loss = nn.functional.mse_loss(x_hat, x)
        # Logging to TensorBoard (if installed) by default
        self.log("train_loss", loss)
        return loss

    def configure_optimizers(self):
        optimizer = optim.Adam(self.parameters(), lr=1e-3)
        return optimizer


# init the autoencoder
autoencoder = LitAutoEncoder(encoder, decoder)
# setup data
dataset = MNIST(os.getcwd(), download=True, transform=ToTensor())
train_loader = utils.data.DataLoader(dataset)
# train the model (hint: here are some helpful Trainer arguments for rapid idea iteration)
trainer = L.Trainer(limit_train_batches=100, max_epochs=700)  # 还改了这里
trainer.fit(model=autoencoder, train_dataloaders=train_loader)

然后跑起来。

我复制粘贴了代码后只改了两处代码，从上图也可以看到对应的两处注释。第一处是为了方便可视化，因为我喜欢通过画图来理解一些概念。第二处只是把 max_epochs 改为了 700，也就是让训练多跑几次。AI 这么笨，一次哪里学的会。

1-2 分钟后，训练应该就跑完了。首先，让我们看一看训练后模型将我们数据集中的图片 encode 后的效果是什么样：

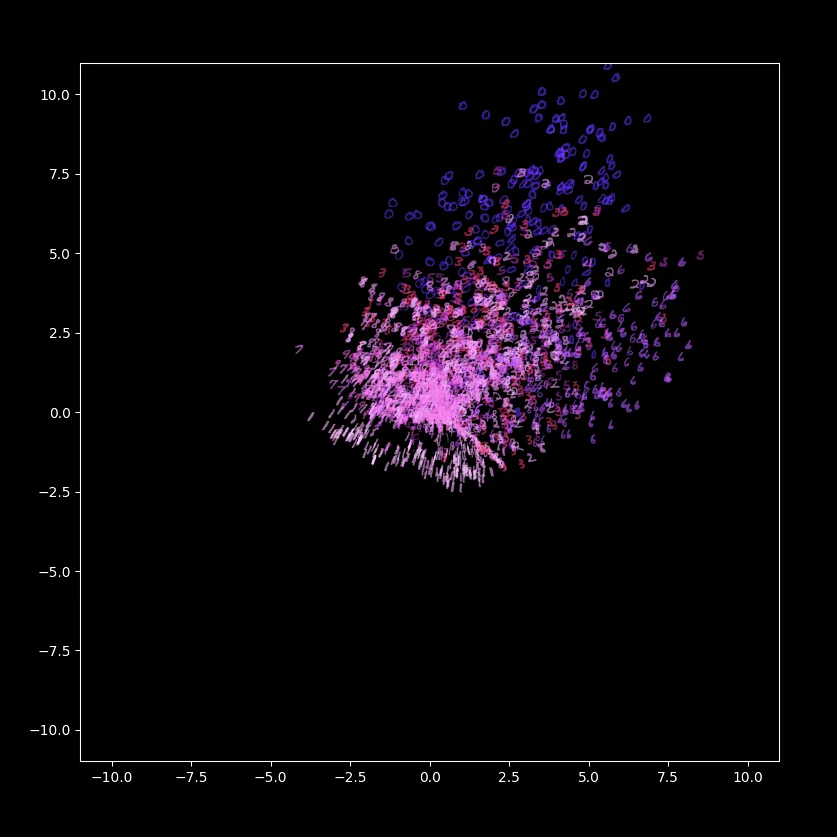
image.png

这张图是这样画出来的：把几百张写着不同的阿拉伯数字的图片喂给模型的 Encoder，每张图都被 “encode” 成了一个二维坐标（这也是为什么在上面的代码里我把 3 改成了 2），把这几百个 “encode” 前对应的阿拉伯数字按对应的二维坐标平铺即可。

我们一般把这也叫作 Latent 空间。

如此简单的一个神经网络，我本以为训练出来的模型会很烂，但得到的效果其实是出乎我意料的：从图内可以看到模型自己学会了在 Latent 空间内聚类，而我们却根本没要求它这样做，我们只是让它在 encode 和 decode 之后可以重新还原出输入的图片而已，由此推测可能模型为了得到最优解，“自然而然”地让 Encoder 产生了这样的特性；此外，在这个空间内，数字“1”和数字“7”其实是挨得很近的，这从另一点说明了模型没有去死记硬背地把答案背下来，而是真的对图形多少有了一些自己的理解！(°ﾛ°٥)

产生这样的效果的一个重要的原因我认为是，这个神经网络虽然简单，但它并不是一个普通的 Autoencoder，把 28x28 的维度“压缩”成一个二维坐标，这是一个非常极端的做法，无意间我们其实训练了一个 *Undercomplete Autoencoder （Jordan, 2018B）*出来。

不过也可以看到这个模型还是有很多的问题存在的。最明显的就是，Latents 在整体向上方和右方偏移，留出了大量不均匀的空隙；再仔细观察一下，虽然“1”和“7”互相落在了附近，但其他图形相近的数字并没有落在相近的位置，如“0”、“6“和”9“等。这些问题直接使得模型无法作为一个生成式AI。

在 Latent 空间内遍历一些点，让 Decoder 去生成图片，就是如下的效果：

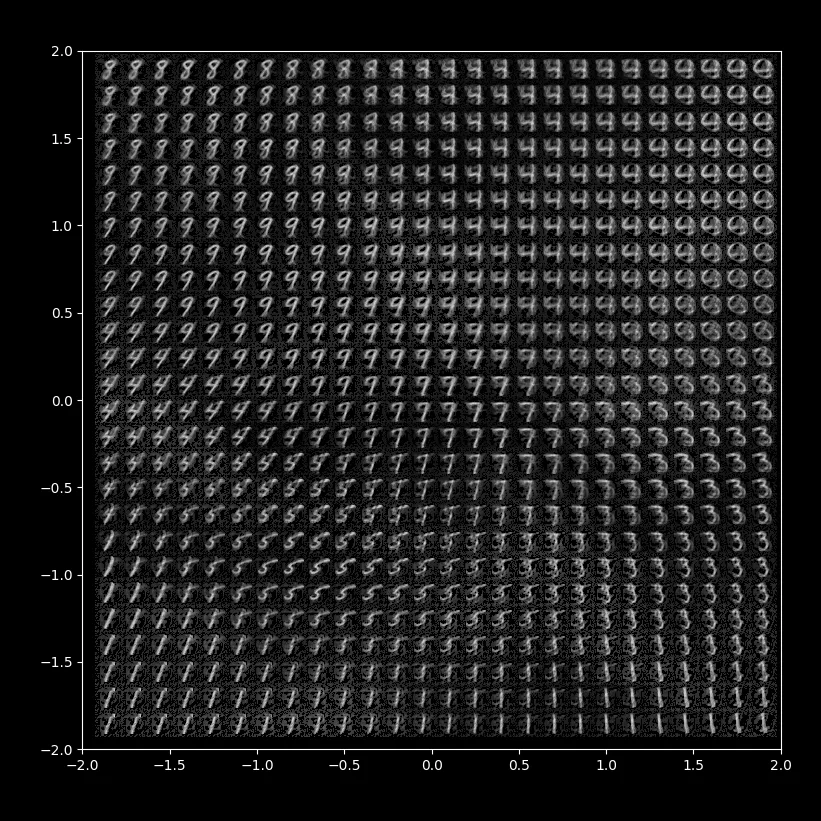
image.png

正如我们所担忧的，在不满足条件的 Latent 空间内直接采样，AI 很容易画出一些莫名其妙的、充满噪音的结果出来。

一个 VAE 的诞生

问题有了。有一位智者曾说过，能提出问题，就已经成功了一半。但你眉头一皱，发现此事并不简单。

我们的输入是一张图片，输出也是一张图片，可我们该怎么通过训练影响神经网络的 Latent 空间的分布呢？提起分布这两个字，很多人可能立马条件反射地想到各种词：随机、概率、正态… 又想到著名的 Central Limit Theorem，万物终为正态分布… 如果我们能够让 Latent 空间分布趋近于一个正态分布，会不会问题就能得到解决？甚至我们可以干脆让它趋近于一个标准正态分布，让 Latent 呈一个平均值 μ 为 0 而平均差 σ 为 1 的分布：

Latent∼N(0,1)Latent \sim \mathcal{N}(0, 1)

可是新的问题来了：如果我们只是硬生生地把上面训练 AE 的二维 Latent 两个数当成 μ 和 σ 去训练肯定不行，这样所有的数字图片不管三七二十一都只会让 μ 为 0 而平均差 σ 为 1，Decoder 完全没有办法去区分不同的图片或数字，我们给到 Decoder 的应该依然是一个二维坐标点而已。好，Encoder 的输出是一个分布，Decoder 想要的是一个坐标点，那我们从 Encoder 的分布中随机取一个点喂给 Decoder，不就好了：

N(0,1)⇒Latent⇒Decoder\mathcal{N}(0, 1) \Rightarrow Latent \Rightarrow Decoder

很多人心想，这题我会，用 Python 有太多办法从正态分布里随机取一个点了。问题是，我们一不小心，给神经网络的运算引入了随机！要知道，我们之所以可以训练一个神经网络，是因为我们可以根据损失函数反向求微分找到每一个参数需要调整的方向和大小，但如果这中间有一个运算结果是随机的，这样的运算就不可微了。

这时候就需要所谓的 Reparameterization Trick 登场了：既然随机的部分是不可微的，那只要与生成随机数相关的部分不涉及任何我们想要训练的参数就好了：

Latent=μ+σ⊙ϵϵ∼N(0,1)\begin{aligned} Latent &= \mu + \sigma \odot \epsilon \\ \epsilon &\sim \mathcal{N}(0, 1) \end{aligned}

如此一来，选出来的点依然是符合分布的，计算 μ 和 σ 的部分没有任何随机，而唯一生成随机的地方 ε 我们又没什么需要训练的，不可微的问题解决了，貌似没有什么能够阻挡，可以开始撸代码了 (｢･ω･)｢

首先，上面 AE 的 Encoder 输出的是一个二维的坐标点，而 VAE 需要 Encoder 输出二维的分布，每一个维度的分布都需要一个平均值 μ 和一个平均差 σ，这就需要输出 4 个数值：

1
2
# encoder = nn.Sequential(nn.Linear(28 * 28, 64), nn.ReLU(), nn.Linear(64, 2))
encoder = nn.Sequential(nn.Linear(28 * 28, 64), nn.ReLU(), nn.Linear(64, 4))

同样，因为现在 Encoder 输出的是二维的分布，需要随机从这个分布里取一个点喂给 Decoder，因此我们新增了一个函数 sample，把我们上面说的 Reparameterization Trick 用一行代码解决：

1
2
3
4
5
6
7
8
9
10
11
12
...
encodered = self.endocder(x)
z = self.sample(encodered)
...

def sample(self, encodered: torch.Tensor) -> torch.Tensor:
    mu = encodered[:, [0, 1]]
    log_var = encodered[:, [2, 3]]
    # reparameterization trick
    std = torch.exp(0.5 * log_var)
    eps = torch.randn_like(std)
    return eps * std + mu

但是你看到代码以后，就知道我骗了你，一行代码解决不了问题。

我还骗了你，我们的 Encoder 输出的也不是平均值 μ 和平均差 σ。

虽然 Reparameterization Trick 实际公式只有一行，对应的代码也只有最后 return 那一行，但我们实际训练时会遇到一个问题：平均差 σ 是一个正数。而这一点我们除非明确写在损失函数里，否则模型是完全不知道这个信息的。所以从代码可以看出，我们的 Encoder 输出的是平均值 μ 和取了对数的方差 logvar。不过这里也只是一个我们用来迁就神经网络训练的 trick，数学上实际是一样的，不信我推倒你就懂了：

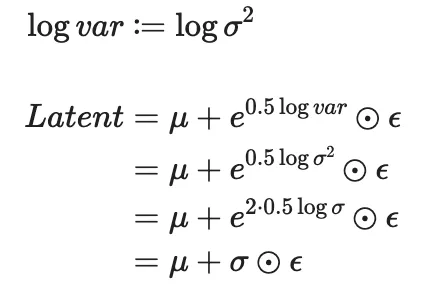
image.png

最后，我们其实还忘记了一件事：怎么能够让模型学会输出标准正态分布？

答案也很明显，就是在损失函数内包含概率分布相关的损失，常用的损失函数就是 KL Divergence：

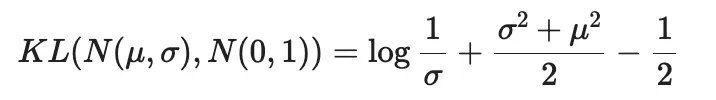
image.png

我们继续套公式：

1
2
3
4
5
mu = encodered[:, [0, 1]]
log_var = encodered[:, [2, 3]]
kld_loss = torch.mean(-0.5 * torch.sum(1 + log_var - mu ** 2 - log_var.exp(), dim=1), dim=0)
kld_weight = 0.0025
loss += kld_weight * kld_loss

（不要问为什么我把参数 kld_weight 设为了 0.0025 之类的问题 (´◔​∀◔`) ）

一系列训练、调参之后，一个标准版 VAE 出炉了：

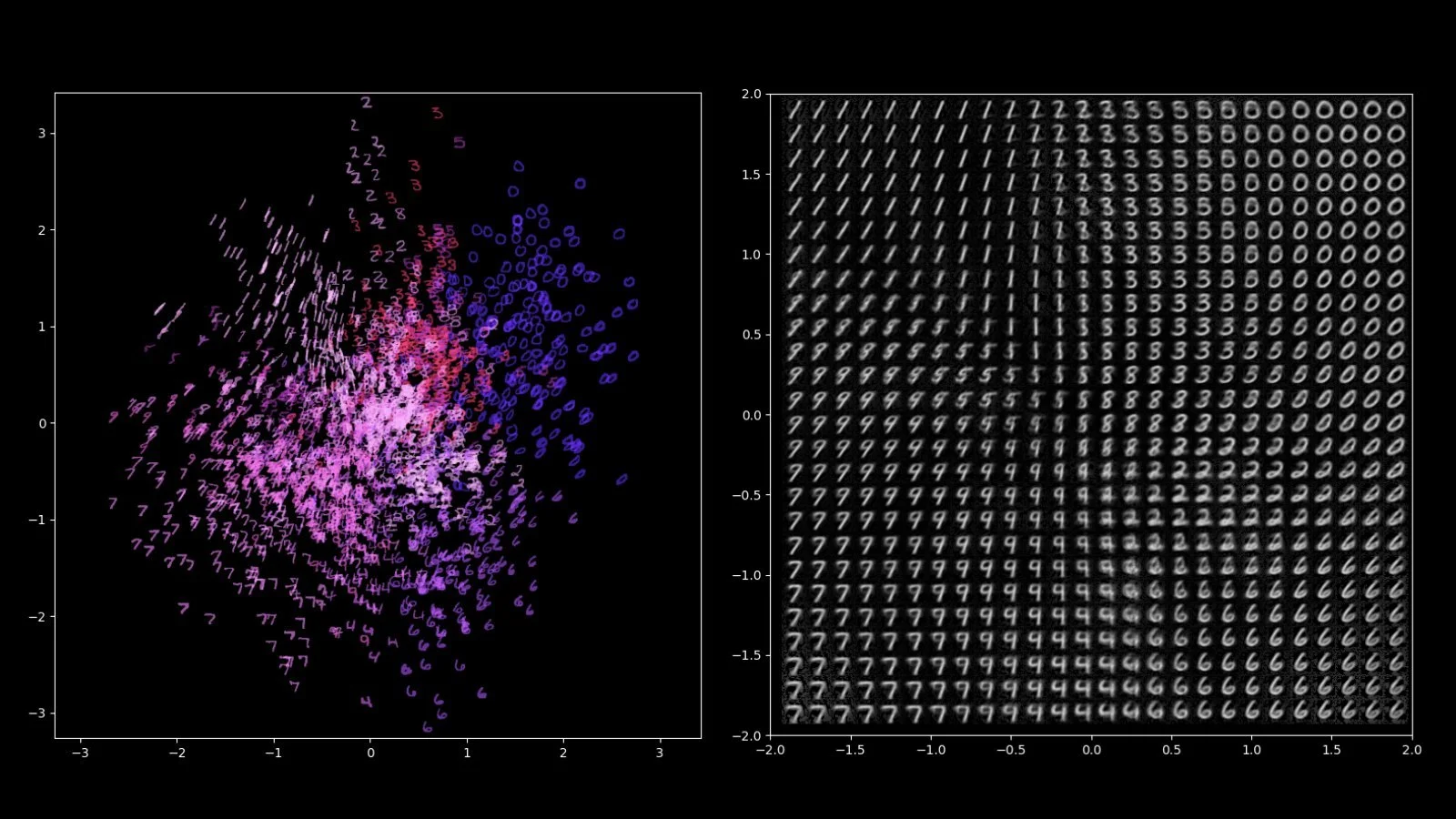
image.png

可以明显地看到，VAE 的 Latent 的空间呈正态分布的样子，不均匀的空隙少了很多，“1” -> “7”、“0” -> “6” 还有 “0” -> “9”等形状相近的数字在 Latent 空间均可见到逐渐变化趋势；而从这样的空间采样喂给 Decoder 去生成图片，已经不会因为 Latent 空间不合理而产生大量不合理的结果了，这意味着 VAE 可以直接作为一个生成式AI。

但我对于结果还不是很满意，比如"0"和“6”还有“9”在 Latent 空间内依然相距较远，再比如其实从右边的图片我们找不到一个写的很好的“4”。

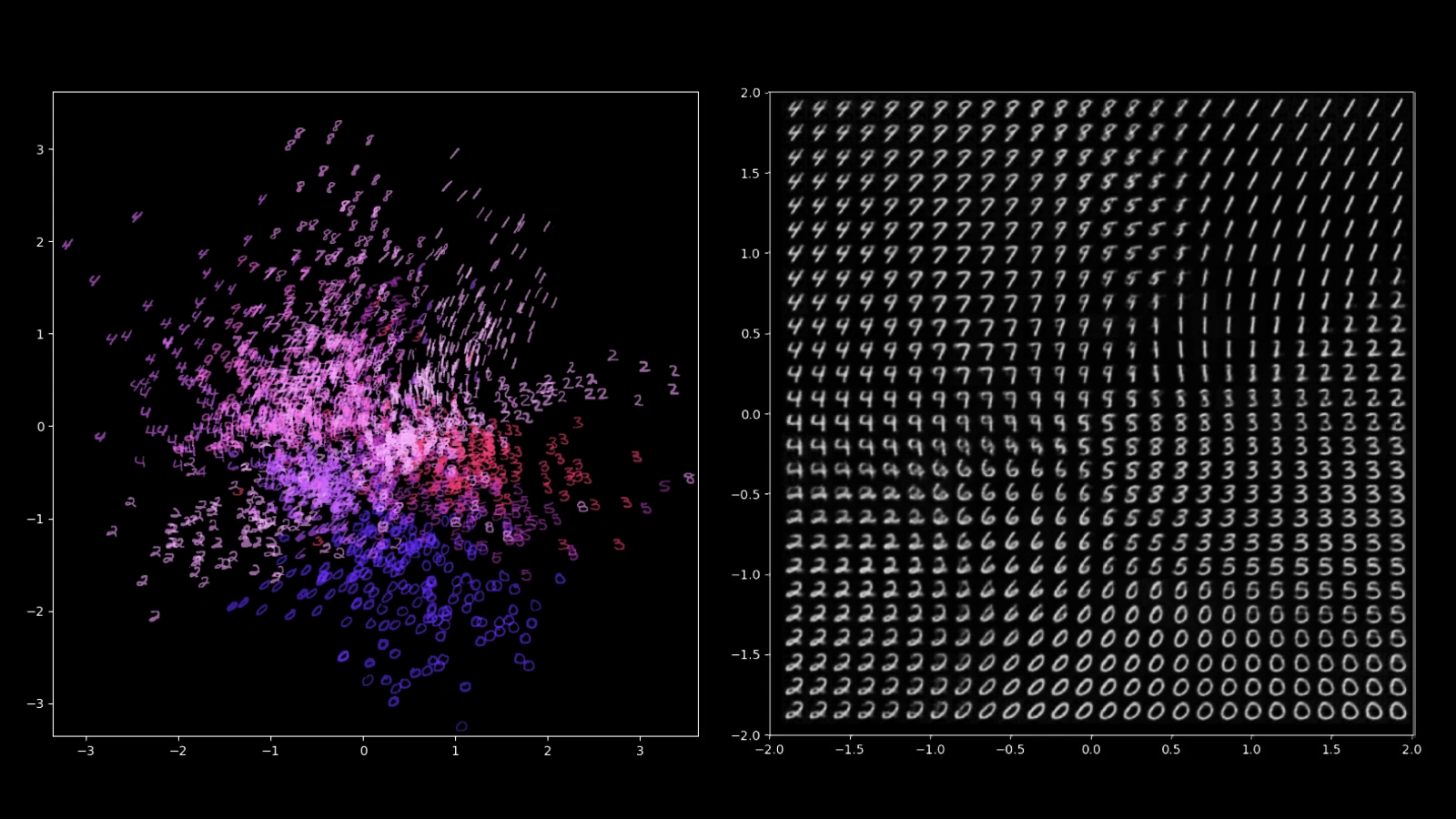
那么如何进一步提升神经网络的性能呢？既然我们在跟图像打交道，怎么可能不试试卷积网络（CNN）！？于是我把上面 Encoder 的两层全连接网络（FCN）换成了8 -> 16 -> 32 -> 64 的四层 CNNs，把输出平均值 μ 和平均差 σ 的地方拆成了两个独立的无激活的 FCNs 让他们各司其职，对应地把 Decoder 也换成 64 -> 32 -> 16 -> 8 的四层 CNNs（没错这是个 UNet），又是一系列训练、调参之后，效果再一次得到了提升，上面提到的一些问题也得到了解决：

image.png

四两拨千斤

虽然手搓了一个 VAE，也看到了 VAE 独有的一些特质，但这就能作为 Stable Diffusion 生成图片和 Sora 生成视频的关键了么？这并不显而易见。

简单算一下生成一张图片需要运算的空间大小： 512 x 512 x 3 = 786,432。这是个近百万数量的空间，要知道即使强如 Llama 2 的 LLM 大模型在处理每一个 token 时所需要面对的也只是屈屈 5,120 的空间（因 Transformer 架构的特殊性，只要 token 长度不是太夸张，往往我们也不需要管到底每次要处理多少个 token，因此这里我认为忽略讨论处理多个 token 对空间的影响是合理的）。更不用说， 这才仅仅是一张512x512像素的小尺寸图片。如果是清晰度 1080P 的长度 1 分钟的视频那就变成了 1920 * 1080 * 3 * 60(s) * 60(FPS) = 22,394,880,000！

从上面的训练可以看到，VAE 处理后的空间是一个漂亮的正态分布，这对于模型尤其是 Diffusion Models 这种概率模型学习掌握真正关键的信息很可能是有益的。而也许更重要的是，正如我们能够把 28 x 28 的图片"压缩"成 2 个数值，Stable Diffusion 的 VAE 可以把图片转化到仅仅 64 x 64 x 4 的 Latent 空间内，从而不需要在像素空间内进行运算了！而 Sora 的 VQ-VAE 更为特殊，不仅是将空间大幅压缩了，而且 VQ-VAE 会把连续的空间压缩成为离散的空间，这就把视频生成问题巧妙地转化成了 OpenAI 一向擅长的文本 token 生成问题了！

Attention is not all you need. You need Latent too!

Reference
Chen, Y., Liu, J., Peng, L., Wu, Y., Xu, Y., & Zhang, Z. (2024). Auto-Encoding variational bayes. Cambridge Explorations in Arts and Sciences, 2(1).
Video generation models as world simulators. (2024). https://openai.com/research/video-generation-models-as-world-simulators
What is a Variational Autoencoder (VAE)? MachineCurve.Com. (2019). https://machinecurve.com/index.php/2019/12/24/what-is-a-variational-autoencoder-vae
Contributors to Wikimedia projects. (2024, February 24). MNIST database. Wikipedia. https://en.wikipedia.org/wiki/MNIST_database
Hussain, S. (2023, July 27). Snawar Hussain. Snawar Hussain. https://snawarhussain.com/blog/genrative models/python/vae/tutorial/machine learning/Reparameterization-trick-in-VAEs-explained/
Jordan, J. (2018A, July 16). Variational autoencoders. Retrieved from https://www.jeremyjordan.me/variational-autoencoders/
Jordan, J. (2018B, March 19). Introduction to autoencoders. Retrieved from https://www.jeremyjordan.me/autoencoders/
Contributors to Wikimedia projects. (2024, March 25). Central limit theorem. Wikipedia. https://en.wikipedia.org/wiki/Central_limit_theorem