Lua 源码解析(二):基本数据类型 —— 表(上)
前言
使用表来统一表示 Lua 中的一切数据,是Lua区分于其他语言的一个特色。这个特色从最开始的Lua版本保持至今,很大的原因是为了在设计上保持简洁。Lua 表分为数组和散列表部分,其中数组部分不像其他语言那样,从0开始作为第一个索引,而是从1开始。散列表部分可以存储任何其他不能存放在数组部分的数据,唯一的要求就是键值不能为nil。尽管内部实现上区分了这两个部分,但是对使用者而言却是透明的。使用Lua表,可以模拟出其他各种数据结构——数组、链表、树等。
table 的结构
表的节点以及表本身的结构均定义在 lobject.h 中:
1 | /* |
在 lua 5.4 版本中,Node 的定义相当地精妙。乍一看,u 与 i_val 分别代表了哈希表中的键值对,非常合理。但是,Node 本身是一个 union 类型!这意味着 u 和 i_val 根本无法同时使用,又该如何作为键值对呢?
这里的关键还在于 NodeKey 结构体的定义:
1 | struct NodeKey { |
NodeKey 的第一个字段就是 TValuefields,大家应该还记得,TValuefields 实际上就是 TValue 结构体中的两个字段:value 和 tt。也就是说 TValuefields 和 i_val 是大小相同的两个字段。
由于 union 共用内存的特点,因此无论是 TValuefields 还是 i_val,实际上都指向 Node 中的同一个位置(此处是 Node 由起始位置开始的一块大小为 TValue 的区域)。这样一来,通过 node.i_val 的方式就可以轻松访问到 Node 中的值,而不用通过 node.u.value_ 或 node.u.tt_ 的方式。
理解了 Node 的结构后,我们再来看 Table 的定义:
1 | typedef struct Table { |
Table 结构体中的 array 和 node 分别代表了表的数组部分和散列表部分。array 是一个 TValue 数组,用于存储表的数组部分。node 是一个 Node 数组,用于存储表的散列表部分,lastfree 用于记录 node 中最后一个空闲的位置,其他字段的含义见注释。
在
table的定义中我们可以发现有lu_byte lsizenode;这样一个字段,它代表的含义为哈希表部分的大小的对数值,而非哈希表本身的大小。这主要是因为 lua 中哈希表的大小永远是 2 的幂次方,这样可以通过位运算来代替取模运算,提高效率。后续我们可以看到许多操作都与这一设定息息相关。
table 的创建与销毁
table 的创建通过 luaH_new 函数实现,外部需要创建一张表时也都直接调用这个函数:
1 | Table *luaH_new (lua_State *L) { |
luaH_new 函数首先通过 luaC_newobj 函数创建了一个新的 Table 对象,再初始化数组以及哈希表的部分。setnodevector 函数用于初始化哈希表部分,其定义如下:
1 | static void setnodevector (lua_State *L, Table *t, unsigned int size) { |
我们仅关注 size == 0 的情况,可以发现这里仅仅是将 t->node 指向一个 dummynode 以及其他字段的初始化。并未真正分配内存。
luaH_new 中对于数组部分的处理也是类似的,仅仅将 t->array 置为 NULL,并未真正分配内存。
table 的销毁通过 luaH_free 函数实现:
1 | void luaH_free (lua_State *L, Table *t) { |
luaH_free 会分别销毁哈希表部分和数组部分,最后销毁 Table 对象本身。
哈希方法
不同类型的哈希方法
在具体介绍 table 中元素的增删查改之前,我们先来看一下 table 中哈希表部分的哈希方法。
在 ltable.c 的起始位置,定义了一些哈希方法的宏:
1 |
|
hashpow2(t, n) 的作用为将 n 通过 lmod 函数对哈希表的大小取模,并返回对应哈希表位置的 Node 指针。
1 | /* |
正是由于哈希表大小永远是 2 的幂次方这一设定,因此可以通过位运算来代替取模运算。
hashstr(t,str) 用于计算字符串的哈希值,可以看到这里直接使用了 str->hash 并取模。
hashboolean(t,p) 与 hashint(t,i) 用于计算布尔值和整数的哈希值,直接取模。
hashmod(t,n) 用于计算一般类型的哈希值,这里为了防止对偶数(哈希表大小)取模会出现的哈希冲突,使用了 ((sizenode(t)-1)|1) 来保证取模的数为奇数。
hashpointer(t,p) 用于计算指针的哈希值,会将指针指向的地址转换为整数再取模。
1 | /* |
较为复杂的就是浮点数的哈希方法了。一言以蔽之,浮点数的哈希方法就是分别取出尾数和指数部分,将二者都转换为整数后相加:
1 |
|
首先,通过 frexp 函数将浮点数转换为尾数和指数部分。这里分解出的尾数是一个 的小数,通过与 -INT_MIN 相乘将其转换为一个整数。指数部分则直接转换为整数。最后将二者相加,得到的结果即为浮点数的哈希值。
frexp是 C 语言中的一个库函数,用于将浮点数分解为尾数和指数部分。frexp函数的原型为double frexp(double x, int *exp);,返回值为尾数,exp为指数。返回值为 的小数,exp为整数。
举例来说,如frexp(3, &exp),则exp为 2,返回值为 0.75。
即 。
mainposition
mainposition 用于计算一个给定的 key 在哈希表中的位置,会在后续的查找、插入等操作中被频繁调用:
1 | /* |
可以看到,这里根据 ktt(Key Type Tag)的不同,分别调用了上述不同类型的哈希方法,并返回对应的 Node 指针。
1 | /* |
此外,提供了一个更加方便的接口 mainpositionTV,用于直接计算 TValue 类型的 key 在哈希表中的位置。
table 的查找
由于 table 中既有数组的部分也有哈希表的部分,因此在查找整型 key 时,需要对两部分分别处理;而对于其他类型的 key,只需要在哈希表部分查找即可。table 对外提供的查找接口为 luaH_get:
1 | /* |
函数中依然是针对不同类型的 key 分别处理。值得注意的是 LUA_VNUMFLT 的处理。假设有如下 Lua 代码:
1 | local t = {} |
可以看出,对于数值等同于一个整数的浮点数键,Lua 会将其视为整数处理,反过来也是如此。在 luaH_get 函数中,通过 luaV_flttointeger 函数判断浮点数是否可以转换为整数,如果可以,则调用 luaH_getint 函数进行查找。
1 | /* |
如果 Key 不属于以上类型,如一般的浮点数、长字符串、布尔值等,会调用 getgeneric 函数进行查找:
1 | /* |
getgeneric 函数首先通过 mainpositionTV 函数计算 key 在哈希表中的位置,然后通过 node.u.next 字段遍历可能的位置,直到找到对应的 key 或遍历到 0 为止。关于 node.u.next 的含义,我们在后续的插入操作中会详细介绍。
luaH_getshortstr 的逻辑与 getgeneric 类似,这里不再赘述。我们再来看一下 luaH_getint 函数:
1 | const TValue *luaH_getint (Table *t, lua_Integer key) { |
可以看到,当 key 的值小于 t->alimit,也即数组部分的长度时,会直接返回数组部分对应下标的值。当 key 的值大于 t->alimit 但 t->alimit 并非数组的实际大小时,会更新 t->alimit 为 key 的值,并依然返回数组部分对应下标的值。否则,会调用 hashint 函数计算 key 在哈希表中的位置,然后通过 node.u.next 字段遍历可能的位置,直到找到对应的 key 或遍历到 0 为止。
这里涉及到数组部分的增长逻辑,这部分依然会在后续的插入操作中详细介绍。这里只需要知道:在查找整型 key 时,会根据查找的下标及数组长度判断 key 属于数组还是哈希表,再到具体的部分中查找。
table 的插入
table 中的元素插入策略较为复杂,这主要是因为 table 既有数组部分又有哈希表部分。在插入元素时,既要决定元素应该放在哪个部分,也要处理二者的扩容问题。且 Lua 中处理哈希冲突的方式部分借鉴了 Brent 优化算法,使得整个流程的代码阅读起来有一定的难度。
关于 Brent 优化算法,可以参考以下资料:
虽然 Lua 中的哈希冲突处理方法借鉴了该算法,但是也做了很多的简化,因此不必深究。
对外接口
table 中提供的插入元素的接口主要有 luaH_set 和 luaH_setint:
1 | /* |
其中 luaH_set 函数是一个通用的接口,用于插入任意类型的 key。该函数会返回插入位置节点对应的 TValue 指针。外部调用者通过对指针的操作,就可以修改对应的值。而 luaH_setint 函数则是专门用于插入整型 key 的接口,并且函数接受一个 TValue* 类型的输入,用于直接将值插入到对应的位置。
这里我们只分析 luaH_set 的逻辑。
可以看到,首先会调用 luaH_get 函数查找 key 对应的位置。如果返回的位置不是 absentkey,则直接返回该位置的 TValue 指针。否则,调用 luaH_newkey 函数插入新的 key,并返回对应位置的 TValue 指针。
luaH_newkey
luaH_newkey 函数用于在哈希表部分插入一个新的 key,由于要处理多种键值类型以及哈希冲突的情况,因此逻辑十分复杂。
node.u.next 的作用
在上文中我们提到,Node 结构体中有一个 next 字段,并且在 luaH_get 函数中会通过 gnext(n) 来获取下一个需要查找的位置。实际上,next 字段是一个用于解决哈希冲突的字段,用于指向下一个哈希值相同但由于冲突而被放置到其他位置的节点,且 next 字段的值是相对于当前节点的偏移量。
初始化时,所有的 next 字段都被置为 0,表示没有冲突。这也是查找过程的终止条件之一:
1 |
|
下文中会将由
next字段连接起来的节点称为冲突链表,这是因为它们的哈希值相同,但由于冲突而被放置到不同的位置。
luaH_newkey 的逻辑
点击展开
1 | /* |
我们先分析一下该函数的整体逻辑:
1 | TValue *luaH_newkey (lua_State *L, Table *t, const TValue *key) { |
首先,声明了一个 Node* 类型的指针 mp,用于存储 key 在哈希表中的位置(即 mainposition),aux 用于存储转换后的整型 key。接着,对 key 的类型进行了判断,如果 key 为 nil,则抛出异常。
即,Lua 中的表不支持
nil作为 key。
1 | else if (ttisfloat(key)) { |
接着,如果 key 为浮点数,会尝试将其转换为整型,如果转换成功,则将 key 替换为转换后的整型 key。如果 key 为 NaN,则抛出异常。
即,Lua 中的表会将值等同于整数的浮点数键视为整数处理。且不支持
NaN作为 key。
1 | mp = mainpositionTV(t, key); |
在处理完上述的两种特殊情况后,调用 mainpositionTV 函数计算 key 在哈希表中的位置。如果该位置已经被占用,或者哈希表为 dummy(即哈希表为空),则需要处理哈希冲突。最后,将 key 插入到计算得到的位置,并返回对应位置的 TValue 指针。
处理哈希冲突
先总体概括一下处理哈希冲突的逻辑:当哈希冲突发生时,会首先尝试找到一个空闲的位置,如果找不到,则会调用 rehash 函数进行哈希表的扩容。接着,会判断冲突节点是否在其主位置,如果不在,则将冲突节点移动到空闲位置,再将新节点插入到主位置;如果在,则直接将新节点插入到空闲位置。
在分析代码之前,先明确一下各个变量的含义:
-
mp:将要插入的 key 在哈希表中的位置(即计算出的哈希值对应的Node指针)。 -
othern:冲突节点本应该在的位置(由于哈希冲突可能会被移动到其他位置)。 -
f:空闲位置。 -
gnext(n):Node结构体中的next字段,用于指向下一个冲突节点。如果next为0,则表示该节点已经是哈希值相同的节点链表的最后一个节点。
-
哈希表中无空闲位置
1
2
3
4
5if (f == NULL) { /* cannot find a free place? */
rehash(L, t, key); /* grow table */
/* whatever called 'newkey' takes care of TM cache */
return luaH_set(L, t, key); /* insert key into grown table */
}此时已经无法插入新的 key 了,只能调用
rehash函数进行哈希表的扩容,再次调用luaH_set函数插入 key。 -
冲突节点不在其主位置
1
2
3
4
5
6
7
8
9
10
11
12if (othern != mp) { /* is colliding node out of its main position? */
/* yes; move colliding node into free position */
while (othern + gnext(othern) != mp) /* find previous */
othern += gnext(othern);
gnext(othern) = cast_int(f - othern); /* rechain to point to 'f' */
*f = *mp; /* copy colliding node into free pos. (mp->next also goes) */
if (gnext(mp) != 0) {
gnext(f) += cast_int(mp - f); /* correct 'next' */
gnext(mp) = 0; /* now 'mp' is free */
}
setempty(gval(mp));
}如果冲突节点不在其主位置,需要将冲突节点移动到空闲位置。首先,找到冲突节点的前一个节点,将其
next指向空闲位置。接着,将冲突节点的值拷贝到空闲位置(这里拷贝的是完整的Node结构体,也包括了next字段)。最后,如果mp之后连接的还有其他的冲突节点,则需要将这些信息都移交给f,并将mp标记为空。 -
冲突节点在其主位置
1
2
3
4
5
6
7
8else { /* colliding node is in its own main position */
/* new node will go into free position */
if (gnext(mp) != 0)
gnext(f) = cast_int((mp + gnext(mp)) - f); /* chain new position */
else lua_assert(gnext(f) == 0);
gnext(mp) = cast_int(f - mp);
mp = f;
}如果冲突节点在其主位置,直接将新节点插入到
f。注意这里改变了连接的方式,会直接将后续的冲突节点连接到f上,再将mp->u.next指向f,相当于将新的节点插在了原有链表的第二个位置。
🌰
为了更直观地理解哈希冲突的处理逻辑,我们通过一个简单的例子来说明,假设我们有一张大小为 8 的哈希表:
-
首先向哈希表中插入元素
A,假设其哈希值为1,则直接插入到哈希表的第一个位置。对应的mp、f以及next如下图所示:
-
这时我们有插入了一个
B元素,假设其哈希值为也为1,则会发生哈希冲突。由于A在其主位置,因此需要将B插入到空闲位置,并且更新对应的next指向。对应的mp、f以及next如下图所示: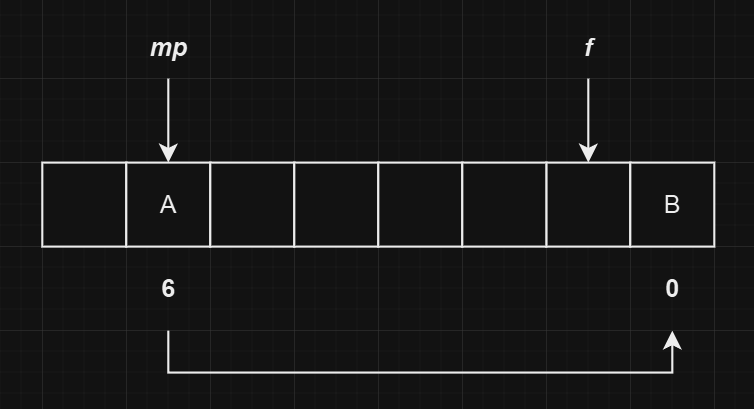
-
我们继续插入一个哈希值为
1的元素C,依然发生哈希冲突。相比于B元素的处理,要额外处理一些新的链表顺序,最终的状态如下图所示: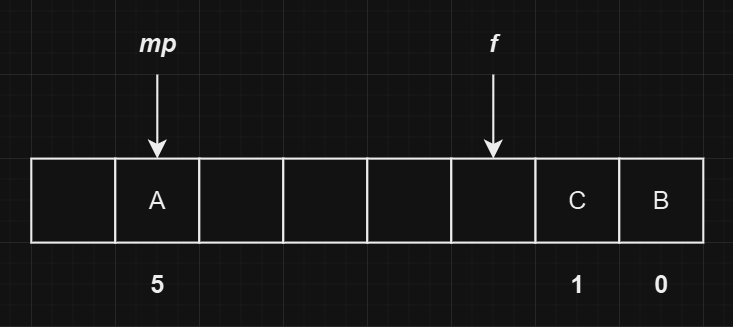
-
继续插入一个哈希值为
1的元素D,最终的状态如下图所示: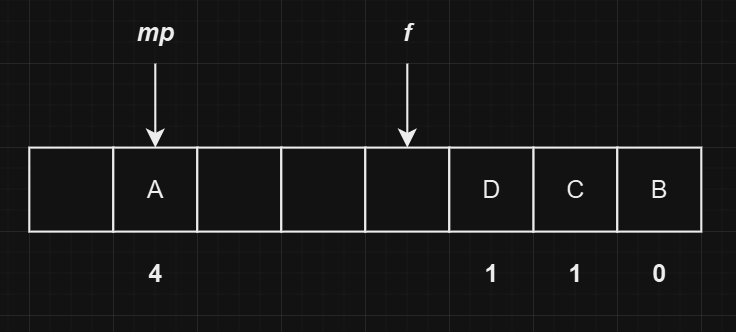
以上展示的是哈希冲突但冲突元素在其主位置的情况,当冲突元素不在其主位置时:
-
假设我们即将插入的元素
E的哈希值为6,则此时的哈希表状态如下图所示: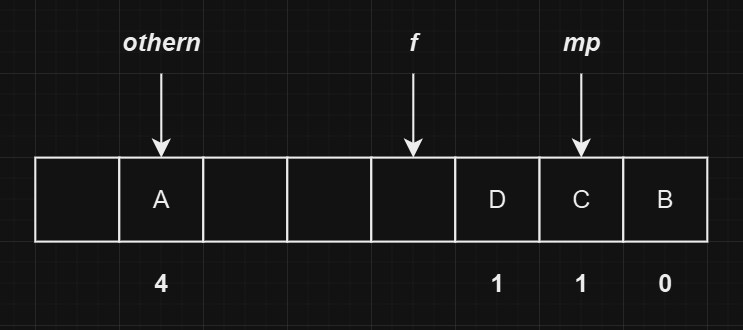
发生冲突的元素为
C,且对应的othern为哈希值1对应的节点。此时就要移动元素C了。 -
首先找到冲突链表中
C的前一个节点,这里为D,然后将C所在位置的内容全部复制到空闲位置,并且更新D的next指向。操作完成后的状态如下图所示: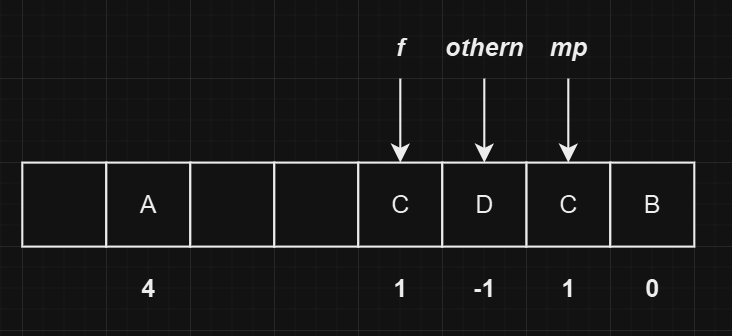
注意这里改变了
othern的位置,现在othern指向D。 -
由于
mp->u.next不为0,即不是冲突链表的最后一个位置,因此需要处理后续的链表顺序。即执行gnext(f) += cast_int(mp - f);操作,最后会将mp->u.next置为0并清空mp的值。最终的状态如下图所示: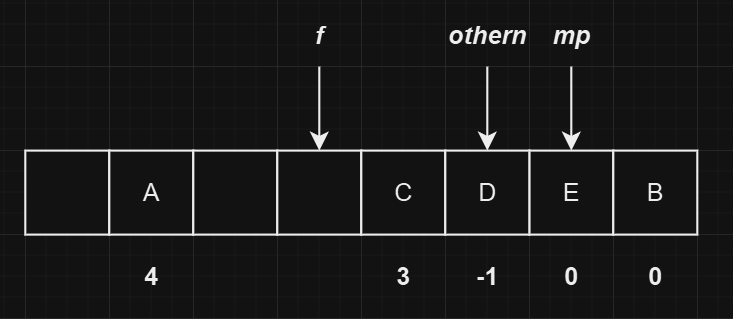
这样也就处理完了冲突元素不在其主位置的情况。
小结
luaH_newkey 主要完成向哈希表部分插入新节点的工作,在处理哈希冲突时,使用了一种简化版本的 Brent 优化算法。当冲突的节点不在其主位置时,会将冲突节点移动到空闲位置,再将新节点插入到主位置;这样可以保证哈希表的查找效率。如果使用原始的开放寻址方式,会导致冲突链过长,查找效率会大大降低。
但这种方法也带来了插入效率的降低,从代码的复杂程度就可见一斑,由于需要处理多种情况以及冲突链的修改,因此插入效率会受到一定的影响。但我们使用哈希表更多地还是用于查询,因此这种牺牲插入效率换取查询效率的方式是值得的。
Array 部分的处理
在分析完 luaH_set 以及 luaH_newkey 函数后,不知道大家会不会有一个疑问:新增加的元素是何时放到数组部分的呢?
或许你会发现:
1 | TValue *luaH_set (lua_State *L, Table *t, const TValue *key) { |
在 luaH_set 函数中,会通过 luaH_get 函数查找 key 是否已经存在;而 luaH_get 在处理整型 key 时,也会从数组部分查找。因此如果插入一个在数组范围之内的 key,那么就会直接返回数组部分对应的 TValue 指针,从而实现了数组部分的插入。
但这个回答也只对了一部分,如果我们继续深究就会发现:
1 | Table *luaH_new (lua_State *L) { |
在 table 初始化时,数组部分是一个空指针,那么我向一张空表中插入的任何元素岂不是都会在哈希表部分?这显然是不合理的。
实际上对于数组部分的处理,都被藏在了 rehash 函数中,在 luaH_newKey 中还有这样一个操作:
1 | TValue *luaH_newkey (lua_State *L, Table *t, const TValue *key) { |
当找不到一个空闲位置时,会调用 rehash 函数进行哈希表的扩容。在 rehash 函数中,会统计表中的所有数字键以及数组部分的使用情况,并依据上述的计算结果,计算出最合适的数组长度,并重新分配所有键的位置。这样就实现了数组部分的插入。
rehash
1 | /* |
首先,rehash 函数声明了一个数组 nums,该数组的长度为 MAXABITS + 1,用于统计表中的所有数字键在不同范围内的分布情况,其中 代表了 的键的数量。
可以看到,这里分别调用 numusearray 和 numusehash 函数统计了数组部分和哈希表部分的键的数量,此外针对 ek 为整型的情况,还会单独计算一次。之后调用 computesizes 函数计算出新的数组部分的大小,并调用 luaH_resize 函数重新分配两部分的空间并重新插入所有的键。
因此,rehash 函数就是表动态分配元素的核心函数,通过该函数,我们可以实现表的哈希表以及数组部分的动态调整。
setlimittosize(重要)
setlimittosize 函数用于将 t->alimit 设置为数组部分的实际大小:
1 | static unsigned int setlimittosize (Table *t) { |
luaH_realasize 函数用于计算数组部分的实际大小:
1 | /* |
可以看出,计算数组部分大小的方式就是返回 , 满足 ,且 。
大家可能会有些费解,为什么在 setlimittosize 函数中调用 luaH_realasize 调整 t->alimit 的值,而 size 本身的计算反而还要依赖于 t->alimit 的值呢?
想要理解这个问题,需要我们对数组部分的大小管理逻辑以及 t->alimit 的真正含义有清晰的了解,先给出结论:
-
Lua 中表的数组部分的实际大小也满足 。
-
t->alimit的含义是数组部分出现的最大的元素的位置,因此必然有 。 -
Lua 中的数组每一个 区间内的元素的数量 都满足 。
因此,当 t->alimit 不在数组的最大长度位置时,它的值一定落在 区间内,这时 就必然是数组部分的实际大小,这也是 luaH_realasize 函数的计算逻辑。
通过上述的分析,我们知道了 t->alimit 并不一定代表数组的实际长度,且一定是一个小于等于数组长度的值,事实上 Lua 提供了一系列宏用于标识这一事件:
1 | /* |
通过 isrealasize 等宏可以快速判断 t->alimit 是否为数组的实际长度。
在进行完空间的重新分配后, t->alimit 会被重新设置为数组部分的实际长度,那么 t->alimit 又是在何时被减小的呢?
答案是 luaH_getn 中,也就是表的长度计算时,可能会将 t->alimit 减小,以方便之后的计算。关于 luaH_getn 函数我们会后续继续讨论。
numusearray
1 | na = numusearray(t, nums); /* count keys in array part */ |
刚刚我们将 t->alimit 恢复到数组部分的实际大小,现在就该统计数组部分的元素的数量了:
1 | /* |
numusearray 函数用于统计数组部分的元素的数量,同时填充 nums 数组,nums[i] 代表了 的键的数量。同时统计所有非空的键的数量并返回。
numusehash
1 | totaluse += numusehash(t, nums, &na); /* count keys in hash part */ |
接下来就是统计哈希表部分的元素的数量:
1 | static int numusehash (const Table *t, unsigned int *nums, unsigned int *pna) { |
该函数会更新三个值,首先会统计哈希表部分的所有元素数量,对应的返回值为 totaluse;其次会将整型键的分布情况更新到 nums 数组中,对应 nums 的输入;最后会将整型键的数量累加到 pna 中。
1 | static int countint (lua_Integer key, unsigned int *nums) { |
countint 就是一个辅助更新 nums 数组的函数,用于统计整型键的分布情况。
computesizes
1 | /* count extra key */ |
在调用 computesizes 之前还有一些操作:针对新插入的键,也就是 ek 为整型的情况,会调用 countint 函数更新 nums 数组,并且更新 na 及 totaluse。
现在,我们统计得到了如下数据:
nums数组:表中所有数字键的分布情况。na:表中所有数字键的数量。totaluse:表中所有键的数量。
现在就该计算新的数组部分大小了 !
1 | /* |
可以看到,computesizes 的逻辑就是根据 nums 数组的数据,找到符合使用率大于 的最大的 值,这个值就是新的数组部分的大小。同时,pna 会被更新为新的数组部分的元素数量。
luaH_resize
1 | /* resize the table to new computed sizes */ |
现在我们得到了数组部分和哈希表部分的新的大小,接下来就是调用 luaH_resize 函数重新分配空间,注意这里 totaluse - na 代表了哈希表部分的元素数量,实际分配的哈希表大小只会更大。
1 | /* |
我们逐步分析:
首先还是声明了一些变量并且计算了旧的数组部分的大小,接着调用 setnodevector 创建了满足 nhsize 大小的新的哈希表部分。
1 | unsigned int i; |
当新的数组长度小于旧的数组长度时,需要将数组部分多出的元素插入到哈希表内,但是可能会出现旧的哈希表空间不足的情况,因此下面的操作中调用了多次的 exchangehashpart 函数,用于在两个哈希表之间交换数据。
为了避免混淆,下文中会分别使用 “新哈希表” 和 “旧哈希表” 来表示两个哈希表。
1 | if (newasize < oldasize) { /* will array shrink? */ |
可以看到,首先将 t->alimit 设置为新的数组部分的大小,这样可以防止之后的 luaH_setint 函数依然把元素插入到数组部分。随后调用 exchangehashpart 函数交换了哈希表部分。此时,t 的哈希表部分为新哈希表,且为空(这保证了插入数组部分多余的元素不会空间不足),而 newt 的哈希表部分则存放了旧哈希表的数据。
接着将数组部分多出的元素插入到 t 的哈希表中,注意此时插入的地方是 新哈希表。
接着将数组部分大小恢复到原来的大小,并且再次交换哈希表部分。此时,t 的哈希表部分又变成了旧哈希表,而 newt 的哈希表部分则是新哈希表,存放了数组部分多出的元素。
1 | /* allocate new array */ |
接着重新分配了数组部分的空间,如果分配失败则释放新哈希表部分的空间并抛出错误,这也是为什么上面要进行第二次的 exchangehashpart 操作的原因。
1 | /* allocation ok; initialize new part of the array */ |
如果分配成功,则再次将 t 的哈希表部分设置为新哈希表,并且将数组部分设置为新的数组部分。接着将新的数组部分的多余部分清空,最后将 newt 的哈希表部分(旧哈希表)的元素重新插入到 t 的哈希表部分中,最后释放 newt 的哈希表部分的空间。
这样也就完成了 luaH_resize 的所有操作。
下面分析一下上述过程中用到的一些函数:
1 | /* |
setnodevector 函数用于创建哈希表部分的空间,当 size 不为零时,可以发现实际上是创建了一个大小为 的哈希表部分。
1 | /* |
reinsert 函数用于将哈希表部分的元素重新插入到新的哈希表部分中,这里使用了前文分析过的 luaH_set 函数。
小结
rehash 函数是表动态分配元素的核心函数,通过该函数,Lua 实现了表的哈希表以及数组部分的动态调整。在 rehash 函数中,通过统计表中的所有数字键以及数组部分的使用情况,计算出最合适的数组长度,并重新分配所有键的位置。
知晓这一原理,对于我们优化 Lua 的性能有很大的帮助,如下述的两段代码:
1 | a = os.clock() |
可以看到,第一段代码的运行时间是第二段代码的两倍多。这是因为第一段代码选择了一个一个向表中插入元素的方式,通过对 rehash 函数的分析我们知道,这样会触发多次 rehash 操作,涉及到空间分配、重新插入等操作,因此效率会大大降低。而第二段代码则直接初始化了一张有一定长度的表,这样就避免了多次的 rehash 操作,因此效率更高。
因此,在我们使用表时,应当尽量避免频繁的插入操作,尽量预分配空间,这样可以提高 Lua 的性能。
table 的长度
在 Lua 中,我们可以使用 # 运算符来获取表的长度,这一功能主要由 luaH_getn 函数实现。
Lua 中这样定义一个表的长度:
表的取长操作返回表的边长(border)。表 t 的边长是一个满足以下条件的非负整数:
1 | (border == 0 or t[border] ~= nil) and (t[border + 1] == nil or border == math.maxinteger) |
简单来说,边长是表的一个正整数索引,它的下个索引刚好在表中不存在,然后再加上两条限制:当索引1不存在时,边长为0;以及所存在的索引值最大为整数值的最大值。注意表中存在的非正整数键不会影响其边长。表长度计算的时间复杂度为,其中的 n 为表中的最大整数键。
在程序中可以通过
__len元函数来更改除字符串之外的任意类型的取长操作。
也就是说,#t 返回的并不是表中元素的个数或者数组部分的长度,而是一个满足上述条件的数字。这个数字与表中键的分布情况有关,使用时经常会让人感到疑惑。例如:
1 | local t1 = {1, 2, nil, 4, 5, 6, nil, nil} |
看上去如此相似的两个表,仅仅因为一个键的差异,#t 的返回值就有很大的区别。让我们来看看 luaH_getn 函数是如何实现的。
查询逻辑
luaH_getn 函数总体按照以下逻辑进行查询:
首先令 limit = t->alimit(注意 t->alimit 并不一定是数组部分的实际长度),然后分以下几种情况进行查询:
-
t[limit]为空这意味着边界一定在
limit之前。首先检查特殊情况:t[limit - 1],如果该项为空则直接返回limit - 1作为边界。否则在 区间内进行二分查找,找到第一个为空的位置即为边界。注意,二分查找意味着该算法并不会遍历所有的元素,因此返回值与表中元素的分布情况关系很大,如上面的例子所示:对于这两张表,二分查找首先都会命中
t[4],t1中这一项不为空,因此会向后查找,直至找到t[6]为空,因而返回值为 6;而t2中t[4]为空,因此会向前查找,最终返回值为 3。 -
t[limit]不为空且limit不为数组实际长度我们假设数组的实际长度为
size,此种情况下会尝试在[limit, size]区间内查找边界。首先还是检查特殊情况:t[limit + 1],如果该项为空则直接返回limit作为边界。否则在 区间内进行二分查找,找到第一个为空的位置即为边界。 -
数组部分为空或
t[size]不为空这种情况下就需要将哈希表部分的长度也考虑在内了,会调用
hash_search来查找哈希表部分的边界,具体的逻辑会在下一节分析。
需要注意的是,luaH_getn 函数在一些情况下会改变 t->alimit 的值以方便下一次的查询,因此在调用该函数之后,t->alimit 的值可能会发生变化。
代码分析
luaH_getn
1 | /* |
我们按照上面的逻辑分析:
1 | lua_Unsigned luaH_getn (Table *t) { |
当 t[limit] (在 C 中则为 array[limit - 1])为空时,首先检查 array[limit - 2] 是否为空,如果为空则直接返回 limit - 1 作为边界。否则在 [0, limit] 区间内进行二分查找,找到第一个为空的位置即为边界。可以看到这种情况下有可能会改变 t->alimit 的值。
此外,在条件判断中可以看到 boundary > luaH_realasize(t) / 2 这样的条件,这是为了保证数组的真实长度一定是大于 t->alimit 的第一个 2 的整数次幂的值。
1 | /* 'limit' is zero or present in table */ |
当 t[limit] 不为空且数组部分还有元素(也就是 !limitequalsasize(t) )时,首先检查 t[limit + 1] 是否为空,如果为空则直接返回 limit 作为边界。否则当 t[limit - 1] 为空时,会在 [limit, size] 区间内进行二分查找,找到第一个为空的位置即为边界。同样,这种情况下也有可能会改变 t->alimit 的值。
1 | /* (3) 'limit' is the last element and either is zero or present in table */ |
最后则会调用 hash_search 函数来查找哈希表部分的边界。
1 | static lua_Unsigned hash_search (Table *t, lua_Unsigned j) { |
在调用 hash_search 函数时,我们已经事先检查了 t[j + 1] 不为空,因此 j 一定是一个存在的索引。hash_search 函数会从 j 开始向后查找,每次将 j 乘以 2,直至找到一个不存在的索引。然后再进行二分查找,找到第一个不存在的索引即为边界。


